
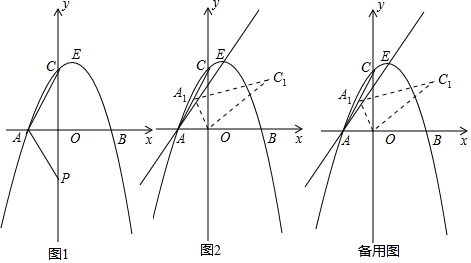
���� ��1�����A��B��C�����������y=ax2+bx+c��ת��Ϊ�ⷽ���鼴�ɣ�
��2�������öԳƣ����߶����ȷ����P��λ�ã��ٸ������������Q�����꼴�ɣ�
��3����A��C1E���ǵ��������Σ�����������ֱ������̼��㼴�ɣ�
��� �⣺��1����A��B���ڶԳ���x=1�Գƣ�A��-2��0����
��B��4��0����
��A��B��C�����������y=ax2+bx+c��$\left\{\begin{array}{l}{c=4}\\{4a-2b+c=0}\\{16a+4b+c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\\{c=4}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2+x+4������E���꣨1��$\frac{9}{2}$����
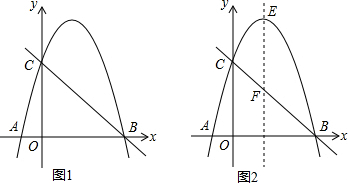
��2�����ڣ��������£�
��ͼ1�У�����A����y��ĶԳƵ�A�䣬��A��G��AC��G��OC��P������AP��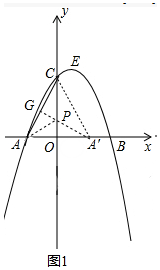
�ɡ�PCG�ס�ACO��$\frac{PG}{OA}$=$\frac{PC}{AC}$��
��OA=2��OC=4��
��AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
��$\frac{PG}{2}$=$\frac{PC}{2\sqrt{5}}$��
��PG=$\frac{\sqrt{5}}{5}$PC��
��PA+$\frac{\sqrt{5}}{5}$PC=PA+PG=A��P+PG=A��G��
���ݴ��߶���̿�֪����P��Ϊ����ĵ㣬
�ɡ�AOP�ס�COA��֪��$\frac{OA}{CO}$=$\frac{OP}{OA}$��
��$\frac{2}{4}$=$\frac{OP}{2}$��
��OP=1��
���P������0��1����
��ͼ2�У��ӳ�BP����������Q����ʱ��QBA=��PBA��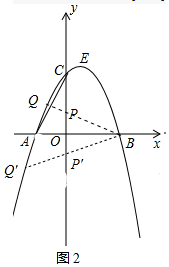
��P��0��1����B��4��0����
��ֱ��PQ�Ľ���ʽΪy=-$\frac{1}{4}$x+1��
��$\left\{\begin{array}{l}{y=-\frac{1}{4}x+1}\\{y=-\frac{1}{2}{x}^{2}+x+4}\end{array}\right.$���$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=\frac{11}{8}}\end{array}\right.$��
���Q��-$\frac{3}{2}$��$\frac{11}{8}$����
��P����x��ĶԳƵ�P�䣬ֱ��BP�佻��������Q�䣬��ʱ��Q��BA=��PBA��
��ֱ��BP��Ľ���ʽΪy=$\frac{1}{4}$x-1��
��$\left\{\begin{array}{l}{y=\frac{1}{4}x-1}\\{y=-\frac{1}{2}{x}^{2}+x+4}\end{array}\right.$���$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=-\frac{13}{8}}\end{array}\right.$��
���Q��������-$\frac{5}{2}$��-$\frac{13}{8}$����
�������������������ĵ�Q���꣨-$\frac{3}{2}$��$\frac{11}{8}$����-$\frac{5}{2}$��-$\frac{13}{8}$����
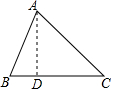
��3����ͼ3�У���A1M��AB��M��C1N��AB��N����AM=x��A1M=2x��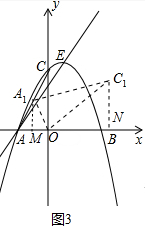
��Rt��AOM1����OA12=OM2+A1M2��
��4x2+��2-x��2=4��
��x=$\frac{4}{5}$��
��A1M=$\frac{8}{5}$��OM=$\frac{6}{5}$��
�ɡ�OA1M�ס�C1OB��
��$\frac{{A}_{1}M}{ON}$=$\frac{OM}{{C}_{1}N}$=$\frac{O{A}_{1}}{O{C}_{1}}$=$\frac{1}{2}$��
��OB=$\frac{16}{5}$��C1N=$\frac{12}{5}$��
��C1��$\frac{16}{5}$��$\frac{12}{5}$����
�ߵ�A��-2��0����E��1��$\frac{9}{2}$����
��AE=5��
��A��E��=AE=$\frac{3\sqrt{13}}{2}$��
��ֱ��AE�Ľ���ʽΪy=$\frac{3}{2}$x+3��
���E�䣨a��$\frac{3}{2}$a+3����
�ߵ�E������ƽ��$\frac{9}{2}$����λ������ƽ��3����λ�õ�A�䣬
��A�䣨a-3��$\frac{3}{2}$a-$\frac{3}{2}$����
��C1E��2=��$\frac{16}{5}$-a��2+��$\frac{12}{5}$-$\frac{3}{2}$a-3��2��
C1A��2=��$\frac{16}{5}$-a+3��2+��$\frac{12}{5}$-$\frac{3}{2}$a+$\frac{3}{2}$��2��
����C1A��=C1E�䣬��C1A��2=C1E��2
������$\frac{16}{5}$-a��2+��$\frac{12}{5}$-$\frac{3}{2}$a-3��2=��$\frac{16}{5}$-a+3��2+��$\frac{12}{5}$-$\frac{3}{2}$a+$\frac{3}{2}$��2��
���a=$\frac{287}{130}$��
��E�䣨$\frac{287}{130}$��$\frac{1641}{260}$����
����A��C1=A��E�䣬
��A��C12=A��E��2
����$\frac{16}{5}$-a+3��2+��$\frac{12}{5}$-$\frac{3}{2}$a+$\frac{3}{2}$��2=$\frac{117}{4}$��
������65a2-482a+488=0��
���a=$\frac{241��3\sqrt{2929}}{65}$��
���E��������$\frac{241+3\sqrt{2929}}{65}$��$\frac{1113+9\sqrt{2929}}{130}$����$\frac{241-3\sqrt{2929}}{65}$��$\frac{1113-9\sqrt{2929}}{130}$����
����E��A��=E��C1��
��E��A��2=E��C12
����$\frac{16}{5}$-a��2+��$\frac{12}{5}$-$\frac{3}{2}$a-3��2=$\frac{117}{4}$��
���a=$\frac{64��9\sqrt{321}}{65}$��
���E������$\frac{64+9\sqrt{321}}{65}$��$\frac{582+27\sqrt{321}}{130}$����$\frac{64-9\sqrt{321}}{65}$��$\frac{582-27\sqrt{321}}{130}$����
�������������������ĵ�E����Ϊ��$\frac{287}{130}$��$\frac{1641}{260}$����$\frac{241+3\sqrt{2929}}{65}$��$\frac{1113+9\sqrt{2929}}{130}$����$\frac{241-3\sqrt{2929}}{65}$��$\frac{1113-9\sqrt{2929}}{130}$����$\frac{64+9\sqrt{321}}{65}$��$\frac{582+27\sqrt{321}}{130}$����$\frac{64-9\sqrt{321}}{65}$��$\frac{582-27\sqrt{321}}{130}$����
���� ���⿼����κ�����Ӧ�á�һ�κ�����Ӧ�á��ȱ������ε��ж������ʡ����ɶ��������������ε����ʵ�֪ʶ���Ȿ��Ĺؼ���ѧ���÷������۵�˼��˼�����⣬ѧ���ù������̽�����⣬����ļ������Ƚϴ���ֵ�Ƚϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x2+1 | B�� | y=2x2+5x | C�� | y=��x-2��2 | D�� | y=x2+2x-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.25��ƽ������0.5 | B�� | -8��-64��һ�������� | ||
| C�� | ��$\sqrt{5}$��2��ƽ�����ǡ�$\sqrt{5}$ | D�� | -1��1������ƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ����в��ϲ������������⣮
�Ķ����в��ϲ������������⣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com