
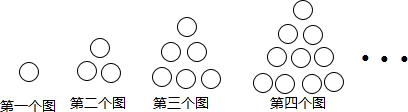
分析 根据已知图形中球的个数,发现第n个图形中球的数量为1+2+3+…+n,据此解答即可.
解答 解:∵第1个图形为1个小圆,即1=$\frac{1}{2}$×1×(1+1),
第2个图形为3个小圆,即3=$\frac{1}{2}$×2×(2+1),
第3个图形为6个小圆,即6=$\frac{1}{2}$×3×(3+1),
第4个图形为10个小圆,即10=$\frac{1}{2}$×4×(4+1),
…
∴第n个图形的小圆的个数为即$\frac{1}{2}$×n(n+1),
故答案为:$\frac{1}{2}$×n(n+1).
点评 此题考查了规律型:图形的变化类,解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:解答题
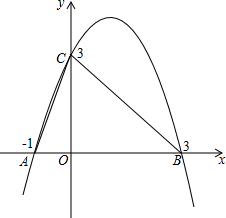 已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3).
已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是2$\sqrt{7}$-2.
如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是2$\sqrt{7}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,2) | B. | (3,4) | C. | (2,-3) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com