
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
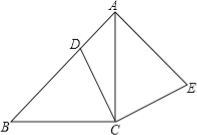
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
【答案】(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论。
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形。
【解析】
(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论。
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形。
证明:(1)∵∠ACB=90°,AC=BC,∴∠B=∠BAC=45°。
∵线段CD绕点C顺时针旋转90°至CE位置,∴∠DCE=90°,CD=CE。
∵∠ACB=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠BCD=∠ACE。
∵在△BCD和△ACE中,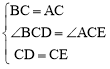 ,
,
∴△BCD≌△ACE(SAS)。∴∠B=∠CAE=45°。
∴∠BAE=45°+45°=90°。∴AB⊥AE。
(2)∵BC2=ADAB,BC=AC,∴AC2=ADAB。∴![]() 。
。
∵∠DAC=∠CAB,∴△DAC∽△CAB。∴∠CDA=∠BCA=90°。
∵∠DAE=90°,∠DCE=90°,∴四边形ADCE为矩形。
∵CD=CE,∴四边形ADCE为正方形。


科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过坐标原点,与
的图象经过坐标原点,与![]() 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
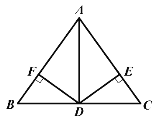
【题目】如图,D是△ABC边BC的中点,DE⊥AC于点E,DF⊥AB于点F,若DE=DF
(1)证明:△ABC的等腰三角形
(2)连接AD,若AB=5,BC=8,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
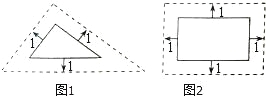
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:
与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:![]() 与y轴交于点C,与抛物线
与y轴交于点C,与抛物线![]() 的另一个交点为D,已知
的另一个交点为D,已知![]() ,P点为抛物线
,P点为抛物线![]() 上一动点(不与A、D重合).
上一动点(不与A、D重合).
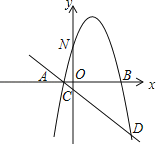
(1)求抛物线和直线l的解析式;
(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作![]() 轴交直线l于点F,求
轴交直线l于点F,求![]() 的最大值;
的最大值;
(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
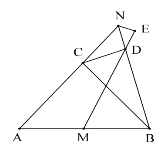
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com