
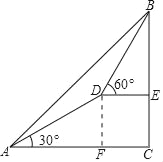
【题目】如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?

【答案】500+500![]()
【解析】试题分析:根据题目所给的度数可判定△ABD是等腰三角形,AD=BD,然后解直角三角形,可求出BE的长和CE的长,从而可求出山高的高度.
试题解析:解:过点D作DF⊥AC.∵∠BAC=45°,∠DAC=30°,∴∠BAD=15°.∵∠BDE=60°,∠BED=90°,∴∠DBE=30°.∵∠ABC=45°,∴∠ABD=15°,∴∠ABD=∠DAB,∴AD=BD=1000.
∵AC⊥BC,DE⊥AC,DE⊥BC,∴∠DFC=∠ACB=∠DEC=90°,∴四边形DFCE是矩形,∴DF=CE.
在Rt△ADF中,∵∠DAF=30°,∴DF=![]() AD=500,∴EC=500,BE=1000×sin60°=
AD=500,∴EC=500,BE=1000×sin60°=![]() ,
,
∴BC=500+![]() 米.
米.
答:山的高度为(500+![]() )米.
)米.


科目:初中数学 来源: 题型:
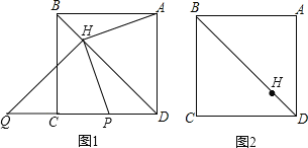
【题目】 已知:在正方形ABCD中,点H在对角线BD上运动(不与B,D重合)连接AH,过H点作HP⊥AH于H交直线CD于点P,作HQ⊥BD于H交直线CD于点Q.
(1)当点H在对角线BD上运动到图1位置时,则CQ与PD的数量关系是______.
(2)当H点运动到图2所示位置时
①依据题意补全图形.
②上述结论还成立吗?若成立,请证明.若不成立,请说明理由.
(3)若正方形边长为![]() ,∠PHD=30°,直接写出PC长.
,∠PHD=30°,直接写出PC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
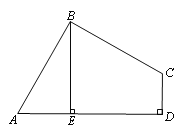
【题目】已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
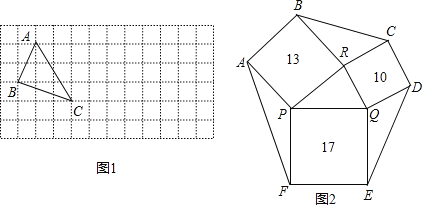
、![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
(1)△ABC的面积为: _________ ;
(2)若△DEF三边的长分别为![]() 、
、![]() 、
、![]() ,请在图1的正方形网格中画出相应的△DEF,并利用构图法求出它的面积;
,请在图1的正方形网格中画出相应的△DEF,并利用构图法求出它的面积;
(3)如图2,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13,10,17,且△PQR、△BCR、△DEQ、△AFP的面积相等,求六边形花坛ABCDEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
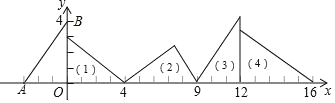
【题目】如图,在直角坐标系中,已知点 A(﹣3,0),B(0,4),对△OAB 连续作旋转变换,依次得到三角形(1),(2),(3),(4)…,则三角形(2019)的直角顶点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面各问题中给出的两个变量x,y,其中y是x的函数的是
① x是正方形的边长,y是这个正方形的面积;
② x是矩形的一边长,y是这个矩形的周长;
③ x是一个正数,y是这个正数的平方根;
④ x是一个正数,y是这个正数的算术平方根.
A. ①②③B. ①②④C. ②④D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 过点
过点![]() ,直线
,直线![]() :
:![]() 与直线
与直线![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.
① 当b=4时,直接写出△OBC内的整点个数;
②若△OBC内的整点个数恰有4个,结合图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,0),B(0,2),C(-4,2),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com