
【题目】如图(1),在△ABC中,AD是BC边的中线,过A点作AE∥BC与过D点作DE∥AB交于点E,连接CE. 
(1)求证:四边形ADCE是平行四边形.
(2)连接BE,AC分别与BE、DE交于点F、G,如图(2),若AC=6,求FG的长. 
【答案】
(1)证明:∵AE∥BC,DE∥AB.
∴四边形ABDE是平行四边形,
∴AE=BD,
又∵BD=DC,
∴AE=DC,
又∵AE∥DC,
∴四边形ADCE是平行四边形
(2)解:∵四边形ADCE是平行四边形,AC=6,
∴AG=GC=3,
又∵AE∥BC,
∴△AEF∽△CBF,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AF=2,
∴FG=AG﹣AF=1
【解析】(1)只要证明AE=CD即可;(2)由AE∥BC,推出△AEF∽△CBF,推出 ![]() =
= ![]() =
= ![]() ,推出AF=2,即可解决问题;
,推出AF=2,即可解决问题;
【考点精析】本题主要考查了平行四边形的判定与性质和相似三角形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1= ![]() 的图象与一次函数y2=
的图象与一次函数y2= ![]() x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=
x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1= ![]() 的图象上.
的图象上. 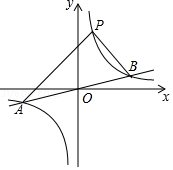
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑自相车旅行越来越受到人们的喜爱,顺风车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%. A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
(1)求今年4月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上A、B两点所表示的数分别为-2和8.
(1)求线段AB的长;
(2)若P为射线BA上的一点(点P不与A、B两点重合,M为PA的中点,N为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A、B两点对应的数为0、10,P为数轴上一点
(1)点P为AB线段的中点,点P对应的数为 .
(2)数轴上有点P,使P到A,B的距离之和为20,点P对应的数为 .
(3)若点P点表示6,点M以每秒钟5个单位的速度从A点向右运动,点N以每秒钟1个单位的速度从B点向右运动,t秒后有PM=PN,求时间t的值(画图写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,AB=AC,点P为边BC上异于B和C的任意一点,过点P作PD⊥AB于D,作PE⊥AC于E,过点C作CF⊥AB于F,求证:PD+PE=CF.

(1)有下面两种证明思路:(一)如图②,连接AP,由△ABP于△ACP面积之和等于△ABC的面积证得PD+PE=CF.(二)如图②,过点P作PG⊥CF,垂足为G,可以证明:PD=GF,PE=CG,则PD+PE=CF.
请你选择其中的一种证明思路完成证明:
(2)探究:如图③,当点P在BC的延长线上时,其它条件不变,探究并证明PD、PE和CF间的数量关系;
(3)猜想:当点P在CB的延长线上时,其它条件不变,猜想PD、PE和CF间的数量关系(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m.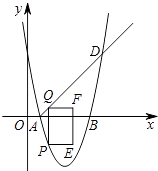
(1)求这条抛物线所对应的函数表达式.
(2)求这条抛物线的对称轴将矩形QPEF的面积分为1:2两部分时m的值.
(3)求d与m之间的函数关系式及d随m的增大而减小时d的取值范围.
(4)当矩形QPEF的对角线互相垂直时,直接写出其对称中心的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.现有 a 根长度相同的火柴棒,按如图 1 摆放时可摆成 m 个正方形,按如图 2摆放时可摆成 2n 个正方形.
(1)试分别用含 m,n 的代数式表示 a;
(2)若这 a 根火柴棒按如图 3 摆放时还可摆成 3p 个正方形.
①试问 p 的值能取 8 吗?请说明理由.
②试求 a 的最小值.
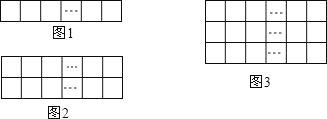
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向,已知射线OB的方向是南偏东m°,射线OC的方向为北偏东n°,且m°的角与n°的角互余.
(1)①若m=60,写出射线OC的方向.(直接回答)
②请直接写出图中所有与∠BOE互余的角及与∠BOE互补的角.
(2)如图2,若射线OA是∠BON的平分线,
①若m=70,求∠AOC的度数.
②若m为任意角度,求∠AOC的度数.(结果用含m的式子表示)
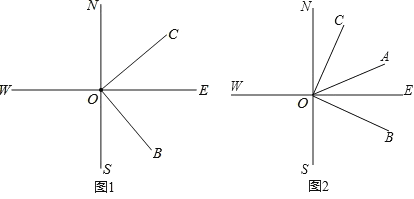
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com