
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
分析 根据三角形的中位线定理首先可以证明:顺次连接四边形各边中点所得四边形是平行四边形.再根据对角线互相垂直,即可证明平行四边形的一个角是直角,则有一个角是直角的平行四边形是矩形.
解答  解:如图,四边形ABCD是菱形,且E、F、G、H分别是AB、BC、CD、AD的中点,
解:如图,四边形ABCD是菱形,且E、F、G、H分别是AB、BC、CD、AD的中点,
则EH∥FG∥BD,EF=FG=$\frac{1}{2}$BD;EF∥HG∥AC,EF=HG=$\frac{1}{2}$AC,AC⊥BD.
故四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EH⊥EF,∠HEF=90°
∴边形EFGH是矩形.
故选:B.
点评 本题考查了中点四边形.能够根据三角形的中位线定理证明:顺次连接四边形各边中点所得四边形是平行四边形;顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形;顺次连接对角线相等的四边形各边中点所得四边形是菱形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
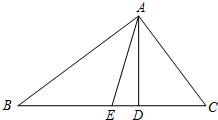 在Rt△ABC中,∠BAC=90°,点E是BC的中点,AD⊥BC,垂足为点D.已知AC=9,cosC=$\frac{3}{5}$.
在Rt△ABC中,∠BAC=90°,点E是BC的中点,AD⊥BC,垂足为点D.已知AC=9,cosC=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,已知E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是AB=AC就可以证明这个多边形是菱形.
如图,在△ABC中,已知E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是AB=AC就可以证明这个多边形是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{1+2y}{3}$ | B. | x=$\frac{1-2y}{3}$ | C. | y=$\frac{3x-1}{2}$ | D. | y=$\frac{1-3x}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 燃灯佛舍利塔(简称燃灯塔)是通州八景之一,该塔始建于南北朝北周宇文时期,距今已有1300多年历史.燃灯塔距运河300米,是通州的象征.某同学想利用相似三角形的有关知识来求燃灯塔的高度.他先测量出燃灯塔落在地面上的影长为12米,然后在同一时刻立一根高2米的标杆,测得标杆影长为0.5米,那么燃灯塔高度为48m米.
燃灯佛舍利塔(简称燃灯塔)是通州八景之一,该塔始建于南北朝北周宇文时期,距今已有1300多年历史.燃灯塔距运河300米,是通州的象征.某同学想利用相似三角形的有关知识来求燃灯塔的高度.他先测量出燃灯塔落在地面上的影长为12米,然后在同一时刻立一根高2米的标杆,测得标杆影长为0.5米,那么燃灯塔高度为48m米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com