
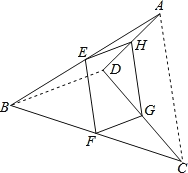
【题目】如图,E、F、G、H分别为四边形ABCD四边之中点.
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足 时,四边形EFGH为菱形.当AC、BD满足 时,四边形EFGH为矩形.当AC、BD满足 时,四边形EFGH为正方形.

【答案】(1)证明见解析;(2)AC=BD;AC⊥BD;AC=BD且AC⊥BD.
【解析】
(1)连接BD,根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD且EH=![]() BD,FG∥BD且FG=
BD,FG∥BD且FG=![]() BD,从而得到EH∥FG且EH=FG,再根据一组对边平行且相等的四边形是平行四边形证明即可;
BD,从而得到EH∥FG且EH=FG,再根据一组对边平行且相等的四边形是平行四边形证明即可;
(2)连接AC,同理可得EF∥AC且EF=![]() AC,再根据邻边相等的平行四边形是菱形,邻边垂直的平行四边形是矩形,邻边相等且垂直的平行四边形是正方形解答.
AC,再根据邻边相等的平行四边形是菱形,邻边垂直的平行四边形是矩形,邻边相等且垂直的平行四边形是正方形解答.
(1)如图,连接BD.
∵E、F、G、H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD且EH=![]() BD,FG∥BD且FG=
BD,FG∥BD且FG=![]() BD,
BD,
∴EH∥FG且EH=FG,
∴四边形EFGH为平行四边形;
(2)连接AC,
同理可得EF∥AC且EF=![]() AC,
AC,
所以,AC=BD时,四边形EFGH为菱形;
AC⊥BD时,四边形EFGH为矩形;
AC=BD且AC⊥BD时,四边形EFGH为正方形.
故答案为:AC=BD;AC⊥BD;AC=BD且AC⊥BD.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,某一时刻,AC=18![]() km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?
km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习之余去买文具,打算购买5支单价相同的签字笔和3本单价相同的笔记本,期间他与售货员对话如下:
小明:您好,我要买5支签字笔和3本笔记本。
售货员:好的,那你应该付52元。
小明:刚才我把两种文具的单价弄反了,以为要付44元。
请你判断在单价没有弄反的情况下,购买1支签字笔和1本笔记本应付()
A. 13元B. 12元C. 11元
D. 10元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求出符合条件的二次函数解析式:
(1)二次函数图象经过点(﹣1,0),(1,2),(0,3);
(2)二次函数图象的顶点坐标为(﹣3,6),且经过点(﹣2,10);
(3)二次函数图象与x轴的交点坐标为(﹣1,0),(3,0),与y轴交点的纵坐标为9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0)、B(2,0)两点,交y轴于点C(0,﹣2),过点A、C画直线.
(1)求二次函数的解析式;
(2)若点P在x轴正半轴上,且PA=PC,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(2k+3)x+k2=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若两不相等的实数根满足![]() -
-![]() -
-![]() =-9,求实数k的值.
=-9,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com