
 和半圆
和半圆 ,其中
,其中 和
和 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 
 ,
, ;
; 和半圆
和半圆 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆 的切线.
的切线.
 ∴∠D
∴∠D F=∠F
F=∠F E.
E. . ………………………….3分
. ………………………….3分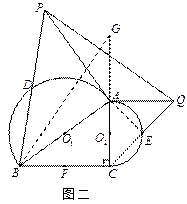 ∵点E是半圆
∵点E是半圆 圆弧的中点,
圆弧的中点,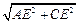 =
=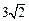 ,
, 的切线,
的切线, (3) 证法一:如图三,设直线FA与PQ的垂足为M,过C作CS⊥MF于S,过B作BR⊥MF于R,连接DR、AD、DM.
(3) 证法一:如图三,设直线FA与PQ的垂足为M,过C作CS⊥MF于S,过B作BR⊥MF于R,连接DR、AD、DM.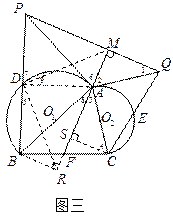 ∵F是BC边的中点,∴
∵F是BC边的中点,∴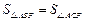 .
.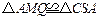 ,
,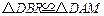 ,
, 直径,
直径,



科目:初中数学 来源:不详 题型:填空题
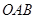 的圆心角
的圆心角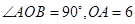 ,点
,点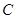 是
是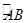 上异于
上异于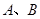 的动点,过点
的动点,过点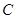 作
作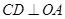 于
于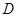 ,作
,作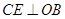 于
于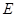 ,连接
,连接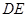 ,点
,点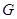 在线段
在线段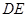 上,且
上,且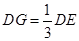 ,连接
,连接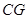 。当点
。当点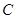 在
在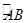 上运动时,在
上运动时,在 中,长度不变的是
中,长度不变的是 ;
;
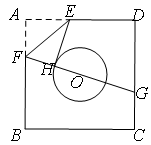
 的边长为
的边长为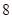 ,⊙
,⊙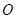 的半径为
的半径为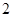 ,圆心
,圆心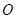 在正方形的中心上,将纸片按图示方式折叠,折叠后点
在正方形的中心上,将纸片按图示方式折叠,折叠后点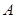 于点
于点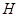 重合,且
重合,且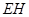 切⊙
切⊙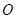 于点
于点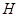 ,延长
,延长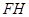 交
交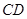 边于点
边于点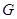 ,则
,则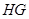 的长为
的长为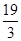 ;
;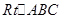 中,
中,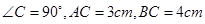 ,则其内心和外心之间的距离是
,则其内心和外心之间的距离是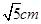 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的直径
的直径 和
和 是它的两条切线,
是它的两条切线, 切
切 于E,交AM于D,交BN于C.设
于E,交AM于D,交BN于C.设 .
.
 ;
; 关于
关于 的关系式;
的关系式; 的面积S,并证明:
的面积S,并证明: .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com