Question

16．某市文博会开幕．开幕前夕，该市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，得到如下数据：
销售单价x（元/件）      …20     30    40    50    60    …
每天销售量（y件）      …500   400   300   200    100   …
（1）把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；
（2）开幕后，市物价部门规定，该工艺品销售单价最高不能超过38元/件，那么销售单价定为多少时，工艺厂销售该工艺品每天获得的利润最大？最大利润是多少？

Answer 1

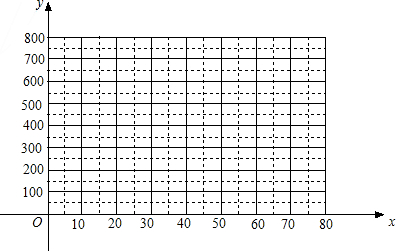
分析 （1）先通过描点得到y与x为一次函数关系，然后利用待定系数法求函数解析式；
（2）利用总利润等于单件利润乘以销售总量得到利润w=（x-10）y=（x-10）（-10x+700），然后利用二次函数的性质求解．

解答 解：（1）如图，

y与x为一次函数关系，设y=kx+b，
把（20，500），（30，400）代入得$\left\{\begin{array}{l}{20k+b=500}\\{30k+b=400}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-10}\\{b=700}\end{array}\right.$，
所以y与x的函数关系式为y=-10x+700；
（2）设利润为w，
w=（x-10）y
=（x-10）（-10x+700）
=-10x²+800x-7000
=-10（x-40）²+9000，
抛物线的对称轴为直线x=40，
∵x≤38，
∴当x=38时，w最大，w的最大值为（38-10）[-10×38+700]=8960（元），
即销售单价定为38时，工艺厂销售该工艺品每天获得的利润最大，最大利润是8960元．

点评 本题考查了二次函数的应用：利用二次函数解决利润问题，在商品经营活动中，经常会遇到求最大利润，最大销量等问题．解此类题的关键是通过题意，确定出二次函数的解析式，然后确定其最大值，实际问题中自变量x的取值要使实际问题有意义，因此在求二次函数的最值时，一定要注意自变量x的取值范围．