
【题目】如图,在正方形![]() 中,
中,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,则图中与
,则图中与![]() 相似的三角形有________.
相似的三角形有________.

【答案】![]() ,
,![]() ,
,![]()
【解析】
利用正方形的性质,运用SAS证明△ABF≌△DAE,再由全等三角形的性质可得出答案.
∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,
∴AF=DE.
在△ABF与△DAE中,
∵ ,
,
∴△ABF≌△DAE(SAS).
∴AE=BF;
∴∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF.
∵∠BAF=90°,
∴∠AFB+∠ABF=90°.
∵∠ABF+∠BAM=90°,
∴∠BAM=∠AFM,
∴△ABM∽△FAM.
同理,△ABM∽△FBA.△ABM∽△AED
故答案为:△ABM∽△FAM,△ABM∽△FBA,△ABM∽△AED.


科目:初中数学 来源: 题型:
【题目】如图①,二次函数的抛物线的顶点坐标C,与x轴的交于A(1,0)、B(﹣3,0)两点,与y轴交于点D(0,3).

(1)求这个抛物线的解析式;
(2)如图②,过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为﹣2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G、H、F四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
(3)如图③,连接AC交y轴于M,在x轴上是否存在点P,使以P、C、M为顶点的三角形与△AOM相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
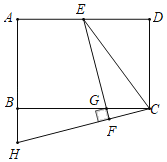
【题目】如图,在长方形ABCD中,点E是AD的中点,连接CE,将△CDE沿着CE翻折得到△CFE,EF交BC于点G,CF的延长线交AB的延长线于点H,若AH=25,BC=40,则FG=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《实数》内容时,我们估算带有根号的无理数的近似值时,经常使用“逐步逼近”的方法来实现的.“逐步逼近”是数学思维方法的一种重要形式,主要通过构造“拟对象”、逐步扩充元素、逐步扩充范围、放缩逼近、合力逼近等方式解决问题.
例如:估算![]() 的近似值时,利用“逐步逼近”法可以得出
的近似值时,利用“逐步逼近”法可以得出![]() .请你根据阅读内容回答下列问题:
.请你根据阅读内容回答下列问题:
(1)![]() 介于连续的两个整数
介于连续的两个整数![]() 和
和![]() ,且
,且![]() ,那么
,那么![]() ______,
______,![]() ______;
______;
(2)![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
(3)已知![]() 的小数部分为
的小数部分为![]() ,
,![]() 的小数部分为
的小数部分为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》已于2019年12月1日起施行,为了解市民对垃圾分类的执行程度,某数学兴趣小组对部分市民进行了问卷调查,调查结果分为“A完全做到”“B基本做到”“C偶尔做到”“D很少做到”四类,该小组绘制的统计图如右:

(1)图中最大的扇形表示调查结果为 的市民占所有被调查市民的 %,这个扇形的圆心角为 °;
(2)你从图中还能得到哪些信息?(写出一条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,动点
,动点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,运动速度均为
同时出发,运动速度均为![]() ,点
,点![]() 沿
沿![]() 运动,到点
运动,到点![]() 停止,点
停止,点![]() 沿
沿![]() 运动,到点
运动,到点![]() 停止
停止![]() 后继续运动,到点
后继续运动,到点![]() 停止,连接
停止,连接![]() ,
,![]() ,
,![]() .设
.设![]() 的面积为
的面积为![]() (这里规定:线段是面积
(这里规定:线段是面积![]() 的几何图形),点
的几何图形),点![]() 的运动时间为
的运动时间为![]() .
.
![]() 填空:
填空:![]() ________
________![]() ,
,![]() 与
与![]() 之间的距离为________
之间的距离为________![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
![]() 直接写出在整个运动过程中,使
直接写出在整个运动过程中,使![]() 与菱形
与菱形![]() 一边平行的所有
一边平行的所有![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A. 2 B. 2或![]() C.
C. ![]() 或
或![]() D. 2或
D. 2或![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜陵市义安区实施了城乡居民基本医疗保险(简称“医疗保险”),办法规定农村村民只要每人每年交纳180元钱就可以加入医疗保险,住院时自己先垫付,出院同时就可得到按一定比例的报销款,这项举措惠及民生,吴斌与同学随机调查了他们镇的一些农民,根据收集到的数据绘制了以下的统计图.
根据图中信息,解答下列问题:
(1)本次调查了多少村民?被调查的村民中参加医疗保险,得到报销款的有多少人?
(2)若该镇有34000村民,请估算有多少人参加了医疗保险?要使两年后参加医疗保险的人数增加到业务31460人,假设这两年的年增长率相同,求年增长率?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com