
分析 根据角的平分线上的点到角的两边的距离相等,再根据三角形的面积公式解答即可.
解答 解:∵一个直角三角形,两边分别为12和16,
∴斜边=$\sqrt{1{2}^{2}+1{6}^{2}}=20$,
因为角的平分线上的点到角的两边的距离相等,
可设该距离为h,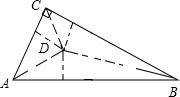
则△ABC的面积=△BCD的面积+△ADC的面积+△ADB的面积=$\frac{1}{2}×BC•h+\frac{1}{2}×AC•h+\frac{1}{2}×AB•h=\frac{1}{2}×AC×BC=\frac{1}{2}×12×16=96$
可得:$\frac{1}{2}•h×(AB+BC+AC)=\frac{1}{2}×(12+16+20)•h=96$,
解得:h=4.
点评 此题考查角平分线,关键是根据角的平分线上的点到角的两边的距离相等分析.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com