
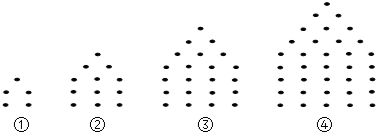
分析 要找这个小房子的规律,可以分为两部分来看:第一个屋顶是1,第二个屋顶是3.第三个屋顶是6.以此类推,第n个屋顶是$\frac{n(n+1)}{2}$.第一个下边是4.第二个下边是9.第三个下边是16.以此类推,第n个下边是(n+1)2个.两部分相加即可得出第n个小房子用的石子数是(n+1)2+$\frac{n(n+1)}{2}$,代入n=10即可确定答案.
解答 解:该小房子用的石子数可以分两部分找规律:
屋顶:第一个是1,第二个是3,第三个是6,…,以此类推,第n个是$\frac{n(n+1)}{2}$;
下边:第一个是4,第二个是9,第三个是16,…,以此类推,第n个是(n+1)2个.
所以共有(n+1)2+$\frac{n(n+1)}{2}$,
当n=10时,原式=121+55=176,
故答案为:176.
点评 本题考查了图形的变化类,分清楚每一个小房子所用的石子个数,主要培养学生的观察能力和空间想象能力.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
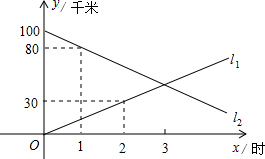 A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地出发,相向而行.假设他们都保持匀速行驶,则他们各自离A地的距离y(千米)都是骑车时间x(时)的一次函数,1小时后乙距离A地80千米;2时后甲距离A地30千米.
A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地出发,相向而行.假设他们都保持匀速行驶,则他们各自离A地的距离y(千米)都是骑车时间x(时)的一次函数,1小时后乙距离A地80千米;2时后甲距离A地30千米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
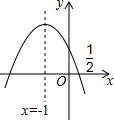 如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)
如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com