
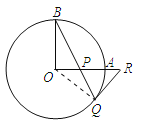
【题目】如图,OA和OB是⊙O的半径,OB=2,OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R.
(1)求证:RP=RQ;
(2)若OP=PQ,求PQ的长.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OQ,由QR为圆O的切线,得到∠OQR为90°,即∠OQB+∠PQR=90°,由OA与OB垂直,根据垂直的定义得到∠BOA=90°,所以∠B+∠BPO=90°,再根据对顶角相等及等角的余角相等,得到∠RPQ=∠RQP,根据“等角对等边”得证;
(2)根据OP=PQ,由“等边对等角”得到∠POQ=∠PQO,又根据半径OB=OQ,再根据“等边对等角”得到∠B=∠BQO,在三角形OBQ中,由∠BOA为直角,设出∠B=∠PQO=∠POQ=x,根据三角形的内角和定理列出关于x的方程,求出方程的解得到x的值,即为∠B的度数,又∠RPQ=∠BPO=60°,PR=QR,所以三角形PRQ为等边三角形,所以PQ=QR,在直角三角形OQR中,根据30°的正切函数定义,由OQ=OB=2,即可求出QR的值,从而得到PQ的长.
(1)连接OQ.∵QR是切线,∴∠OQR=90°,∴∠BQO+∠PQR=90°.
∵OA⊥OB,∴∠BOA=90°,∴∠B+∠BPO=90°,又∠BPO=∠RPQ,∴∠B+∠RPQ=90°.
由OB=OQ得:∠B=∠BQO,∴∠RPQ=∠RQP,∴PR=QR;
(2)∵OP=PQ,∴∠POQ=∠PQO,
又OB=OQ,∴∠B=∠PQO,
设∠B=∠PQO=∠POQ=x,又∠BOP=90°,
根据三角形内角和定理得:
∠B+∠BOP+∠POQ+∠PQO=180°,即x+90°+x+x=180°,
解得:x=30°,即∠B=30°,∴∠RPQ=∠BPO=60°,又PR=QR,∴△PQR为等边三角形,即PQ=QR=PR,
在直角三角形OQR中,OQ=OB=2,
根据锐角三角函数定义得:
![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两名采购员去同一家饲料公司分别购买两次饲料,两次购买饲料价格分别为m元/千克和n元/千克,且m≠n,两名采购员的采购方式也不同,其中甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?(用字母m、n表示)
(2)谁的购货方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边![]() 边长为8cm,点
边长为8cm,点![]() 是
是![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上运动,以
上运动,以![]() 为边在
为边在![]() 右侧作等边
右侧作等边![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)当点![]() 在线段
在线段![]() (不包括端点
(不包括端点![]() )上时,求证:
)上时,求证:![]() ;
;
(2)求证:![]() 平分
平分![]() ;
;
(3)连接![]() ,点
,点![]() 在移动过程中,线段
在移动过程中,线段![]() 长的最小值等于 (直接写出结果)
长的最小值等于 (直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com