�Ķ����²��ϲ���գ�
ƽ������n���㣨n��2���������������㲻��ͬһֱ���ϣ�����Щ����ֱ�ߣ�һ����������������ͬ��ֱ�ߣ�
��1��������������������ʱ��������1��ֱ�ߣ�
����3����ʱ��������3��ֱ�ߣ�
����4����ʱ��������6��ֱ�ߣ�
����5����ʱ��������10��ֱ�ߣ�
��
��2�����ɣ������ĸ���n�Ϳ�����ֱ�ߵ�����S
n�����֣�
��3��������ƽ������n���㣬����ȷ��һ��ֱ�ߣ�ȡ��һ����A��n��ȡ����ȡ�ڶ�����B�У�n-1����ȡ��������һ��������n��n-1����ֱ�ߣ���AB��BA��ͬһ��ֱ�ߣ���Ӧ����2����
Sn=��
��4�����ۣ�
Sn=��
| ��ĸ��� |
������ֱ������ |
| 2 |
l=S2= |
| 3 |
3=S3= |
| 4 |
6=S4= |
| 5 |
10=S5= |
| �� |
�� |
| n |
Sn= |
��̽���������⣺
ƽ������n��n��3�����㣬���������㲻��ͬһֱ���ϣ������������������Σ�һ�����������ٲ�ͬ�������Σ�
�ٷ�����
������3����ʱ������
��������
����4����ʱ������
��������
����5����ʱ������
��������
��
�ڹ��ɣ������ĸ���n�Ϳ������������εĸ���S
n�����֣�
| ��ĸ��� |
������������� |
| 3 |
|
| 4 |
|
| 5 |
|
| �� |
�� |
| n |
|
��������
ȡ��һ����A��n��ȡ����
ȡ�ڶ�����B�У�n-1����ȡ����
ȡ��������C�У�n-2����ȡ����
����ABC����ACB����BAC����BCA����CAB����CBA��ͬһ�������Σ���Ӧ����6��
�ܽ��ۣ�
��




 ��
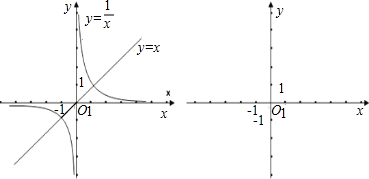
�� ����ͬһֱ������ϵ�л��������������IJ�ͼ��
����ͬһֱ������ϵ�л��������������IJ�ͼ�� �����
����� ��
�� ������ͼ��Ľ���Ϊ��1��1���ͣ�-1��-1��
������ͼ��Ľ���Ϊ��1��1���ͣ�-1��-1�� ��1��������������õ���ѧ˼�뷽����______��
��1��������������õ���ѧ˼�뷽����______�� ʱ��x��ȡֵ��Χ��______��
ʱ��x��ȡֵ��Χ��______�� ����Ҫ����ͼ��
����Ҫ����ͼ��