
分析 (1)根据题意每次输入都是与前一次运算结果求差后取绝对值,将已知数据输入求出即可;
(2)根据题意可得出只有3个数字,当最后输入最大值时结果得到的值最大,当首先将最大值输入则结果是最小值,进而分析得出即可.
解答 解:(1)根据题意可以得出:|1-2|=|-1|=1,
|1-3|=|-2|=2,
|2-4|=|-2|=2,
对于1,2,3,4,按如下次序|||1-3|-4|-2|=0,
|||1-3|-2|-4|=4,
故全部输入完毕后显示的结果的最大值是4,最小值是0;
故答案为:2,4,0;
(2)∵随意地一个一个的输入三个互不相等的正整数2,a,b,全部输入完毕后显示的最后结果设为k,k的最大值为10,
∴设b为较大数字,当a=1时,|b-|a-2||=|b-1|=10,
解得:b=11,
故此时任意输入后得到的最小数为:|2-|11-1||=8,
设b为较大数字,当b>a>2时,|b-|a-2||=|b-a+2|=10,
则b-a+2=10,即b-a=8,则a-b=-8,
故此时任意输入后得到的最小数为:|a-|b-2||=|a-b+2|=6,
综上所述:k的最小值为6.
点评 此题考查了绝对值,虽然以计算为载体,注意要有试验观察和分情况讨论的能力.


科目:初中数学 来源: 题型:解答题
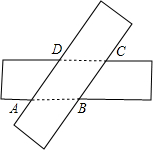 把两张宽度相等的矩形纸片叠放在一起,得到如图的四边形ABCD.
把两张宽度相等的矩形纸片叠放在一起,得到如图的四边形ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
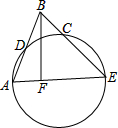 已知如图:D是⊙O劣弧AC的中点,连结AD并延长AD到B,使DB=AD,连结BC并延长交⊙O于E,连结AE,BF⊥AE于F.
已知如图:D是⊙O劣弧AC的中点,连结AD并延长AD到B,使DB=AD,连结BC并延长交⊙O于E,连结AE,BF⊥AE于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
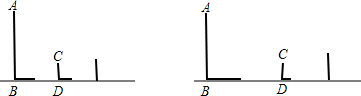
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
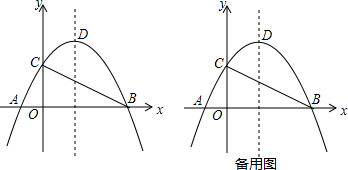
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com