
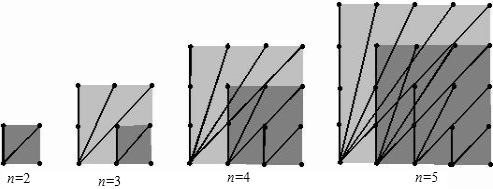
探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:

当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1,![]() ,2,
,2,![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5。
五种,比n=2时增加了3种,即S=2+3=5。
(1) 观察图形,填写下表:
| 钉子数(n×n) | S值 |
| 2×2 | 2 |
| 3×3 | 2+3 |
| 4×4 | 2+3+( ) |
| 5×5 | ( ) |
(2) 写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式。
科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 5 |
| 2 |
| 钉子数(n) | S值 |
| 2×2 | 2 |
| 3×3 | 2+3 |
| 4×4 | 2+3+( ) |
| 5×5 | ( ) |
查看答案和解析>>
科目:初中数学 来源:2013届北京101中学八年级下学期期中考试数学试卷(解析版) 题型:填空题
如图,探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:当n=2时,钉子板上所连不同线段的长度值只有1与 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;那么当n=5时,
S=_________;对n×n的钉子板,写出用n表示S的代数式S=_____________________。
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;那么当n=5时,
S=_________;对n×n的钉子板,写出用n表示S的代数式S=_____________________。

n=2 n=3 n=4 n=5
第16题图
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2; ,2,
,2, ,2
,2 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
| 钉子数(n) | S值 |
| 2×2 | 2 |
| 3×3 | 2+3 |
| 4×4 | 2+3+ |
| 5×5 |
查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;当n=3时,钉子板上所连不同线段的长度值只有1,
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;当n=3时,钉子板上所连不同线段的长度值只有1,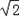 ,2,
,2, ,2
,2 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com