解:(1)∵a=1,b=-(m-2),c=

,
∴△=b
2-4ac=[-(m-2)
2]-4×1×(

)
=2m
2-4m+4=2(m-1)
2+2>0,
∴方程总有两个不相等的实数根;
(2)∵a=1,b=-(m-2),c=-
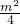
,
∴x
1+x
2=m-2,
∵方程总有两个的实数根
∴x
1•x
2=-
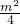
≤0,
∴x
1与x
2异号或有一个为0,由|x
2|=|x
1|+2,|x
2|-|x
1|=2,
当x
1≥0,x
2<0时,-x
2-x
1=2,即-(m-2)=2,解得m=0,
此时,方程为x
2+2x=0,解得x
1=0,x
2=-2;
当x
1≤0,x
2>0时,x
2+x
1=m-2=2,解得m=4,
当m=4时,x
2-2x-4=0,
∴x
1=1-

,x
2=1+

.
分析:(1)根据方程根的判别式判断根的情况,只要证明判别式△的值恒为正值即可;
(2)|x
2|=|x
1|+2,即|x
2|-|x
1|=2,两边平方后再配方得(x
1+x
2)
2-4|x
1x
2|=4,再根据根与系数的关系用m表示出两根的和与两根的积,代入得到关于m的方程,即可求得m的值.
点评:总结一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
此题不仅考查了根的判别式的应用,还应用了根与系数的关系以及配方法的运用,增根的判断.

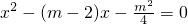
 ,
, )
)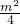 ,
,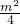 ≤0,
≤0, ,x2=1+
,x2=1+ .
.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案