Question

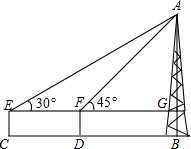
18．周末，小明和小华来滨湖新区渡江纪念馆游玩，看到高雄挺拔的“胜利之塔”，萌发了用所学知识测量塔高的想法，如图，他俩在塔AB前的平地上选择一点C，树立测角仪CE，测出看塔顶的仰角约为30°，从C点向塔底B走70米到达D点，测出看塔顶的仰角约为45°，已知测角仪器高为1米，则塔AB的高大约为（$\sqrt{3}$≈1.7）（　　）

• A． 141米
• B． 101米
• C． 91米
• D． 96米

Answer 1

分析 首先设AG=x米．本题涉及到两个直角三角形△AGF、△AGE，应利用其公共边AG构造等量关系，借助EF=CD=EG-FG=70米，构造方程关系式，进而可求出答案．

解答 解：设AG=x米．
在Rt△AGF中，∵∠AGF=90°，∠AFG=45°，
∴FG=AG=x米，
同理在Rt△AEG中，∵∠AGE=90°，∠AEG=30°，
∴EG=$\sqrt{3}$AG=$\sqrt{3}$x米．
∵EF=EG-FG，
∴$\sqrt{3}$x-x=70，
解可得：x=35（$\sqrt{3}$+1）≈94.5；
故AB=AG+BG≈94.5+1≈96．
答：塔AB的高大约为96米．
故选D．

点评 本题考查解直角三角形的应用-仰角俯角问题，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．