
【题目】![]() 是
是![]() 的直角三角形,
的直角三角形,![]() 的中点分别是点
的中点分别是点![]() 点
点![]() ,动点
,动点![]() 从点
从点![]() 出发,按箭头方向通过
出发,按箭头方向通过![]() 到
到![]() ;以
;以![]() 的速度运动,设
的速度运动,设![]() 点从
点从![]() 开始运动的距离为
开始运动的距离为![]() ,
,![]() 的面积为
的面积为![]() 试回答以下问题:
试回答以下问题:
(1)![]() 点从
点从![]() 出发到
出发到![]() 停止,写出
停止,写出![]() 与
与![]() 的函数关系式并写出
的函数关系式并写出![]() 的取值范围.
的取值范围.
(2)求出![]() 点从
点从![]() 出发后几秒时,
出发后几秒时,![]()

【答案】(1)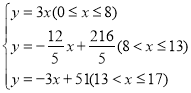 ;(2)点P从点B出发2秒或15秒时,
;(2)点P从点B出发2秒或15秒时,![]()
【解析】
(1)利用勾股定理求出AC,根据中点的性质求出CN、MN,再根据点P在BC边上,CN边上和MN边上时,分别求出函数解析式;
(2)先求出△ABC的面积根据![]() 求出△ABP的面积,再分别代入函数解析式,解出符合取值范围的x值即是答案.
求出△ABP的面积,再分别代入函数解析式,解出符合取值范围的x值即是答案.
(1)在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() 的中点分别是点
的中点分别是点![]() 点
点![]() ,
,
∴CN=![]() AC=5,MN=
AC=5,MN=![]() BC=4,
BC=4,
当点P在BC边上即![]() 时,BP=x,∴
时,BP=x,∴![]() ;
;
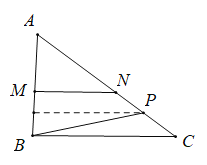
当点P在CN边上即![]() 时,如图:过点P作PH⊥AB于H,连接BP,
时,如图:过点P作PH⊥AB于H,连接BP,
∴∠AHP=∠B=90°,
∴HP∥BC,
∴∠APH=∠C,
∵AP=18-x,cos∠C=![]() ,
,
∴HP=![]() ,
,
∴![]() ;
;
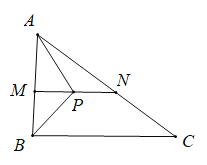
当点P在MN边上即![]() 时,如图:MP=17-x,
时,如图:MP=17-x,
∴![]()
综上,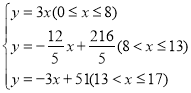 ;
;
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 时,3x=6,解得x=2,符合题意;
时,3x=6,解得x=2,符合题意;
当![]() 时,
时,![]() ,解得x=15.5>13,舍去;
,解得x=15.5>13,舍去;
当![]() 时,
时,![]() ,解得x=15,符合题意,
,解得x=15,符合题意,
∴点P从点B出发2秒或15秒时,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形:
(2)若菱形ABEF的周长为16,∠BEF=120°,求AE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的位置如图所示.
的位置如图所示.
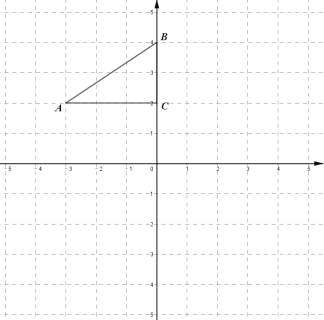
(1)画出![]() 先向右平移3个单位,再向下平移6个单位后得到的
先向右平移3个单位,再向下平移6个单位后得到的![]() ,并写出
,并写出![]() ,各顶点的坐标;
,各顶点的坐标;
(2)画出![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到的
后得到的![]() ,并写出
,并写出![]() ,各顶点的坐标.
,各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
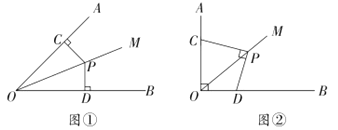
【题目】已知![]() 是
是![]() 的平分线,点
的平分线,点![]() 是射线
是射线![]() 上一点,点C、D分别在射线
上一点,点C、D分别在射线![]() 、
、![]() 上,连接PC、PD.
上,连接PC、PD.
(1)发现问题
如图①,当![]() ,
,![]() 时,则PC与PD的数量关系是________.
时,则PC与PD的数量关系是________.
(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当![]() 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
时,PC与PD在(1)中的数量关系还成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
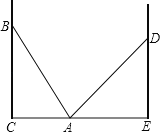
【题目】如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,点B到地面的垂直距离BC=5![]() 米,DE=6米.
米,DE=6米.
(1)求梯子的长度;
(2)求两面墙之间的距离CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商贸公司有![]() 、
、![]() 两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
体积(立方米/件) | 质量(吨/件) | |
| 0.8 | 0.5 |
| 2 | 1 |
(1)已知一批商品有![]() 、
、![]() 两种型号,体积一共是20立方米,质量一共是10.5吨,求
两种型号,体积一共是20立方米,质量一共是10.5吨,求![]() 、
、![]() 两种型号商品各有几件?
两种型号商品各有几件?
(2)物资公司现有可供使用的货车每辆额定载重3.5吨,容积为6立方米,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
现要将(1)中商品一次或分批运输到目的地,如果两种收费方式可混合使用,商贸公司应如何选择运送、付费方式,使其所花运费最少,最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知![]() ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如![]() 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.

请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”![]() ,必有实数根;
,必有实数根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6![]() ,求ABC 的面积.
,求ABC 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com