
【题目】如图,在△ABC中,AB=AC,BC=8,tanB=![]() ,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.
,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.
【答案】![]()
【解析】分析:如图,作AE⊥BC于E,DK⊥BC于K,连接BB′交CD于H.只要证明∠AB′B=90°,求出AB、BB′,理由勾股定理即可解决问题;
详解:如图,作AE⊥BC于E,DK⊥BC于K,连接BB′交CD于H.
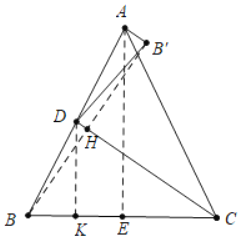
∵AB=AC,AE⊥BC,
∴BE=EC=4,
在Rt△ABE中,∵tanB=![]() ,
,
∴AE=6,AB=![]() =2
=2![]() ,
,
∵DK∥AE,BD=AD,
∴BK=EK=2,
∴DK=![]() AE=3,
AE=3,
在Rt△CDK中,CD=![]() ,
,
∵B、B′关于CD对称,
∴BB′⊥CD,BH=HB′
∵S△BDC=![]() BCDK=
BCDK=![]() CDBH,
CDBH,
∴BH=![]() ,
,
∴BB′=![]() ,
,
∵BD=AD=DB′,
∴∠AB′B=90°,
∴AB′=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,弧CD=弧CE.
(1)求证:OA=OB
(2)已知AB=4![]() ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,其中种茄子每亩可获利2400元,种西红柿每亩可获利2600元,王大伯一共获纯利多少元.
(1)若设种茄子x亩,用含有x的式子填下表:
亩数 | 每亩可获利 | 总获利 | |
茄子 | |||
西红柿 |
(2)王大伯种两种蔬菜一共获纯利多少元.(用含x的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
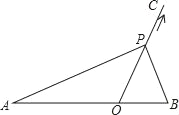
【题目】如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为( )
A. ![]() B.
B. ![]() C. 1或
C. 1或![]() D. 1或
D. 1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
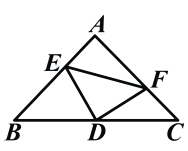
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
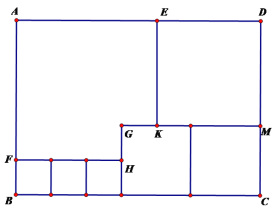
【题目】如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成大长方形ABCD,其中GH=1,GK=1,设BF=a.
(1)用含a的代数式表示CM=_____cm,DM=_______cm.
(2)用含a的代数式表示大长方形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
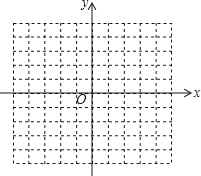
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD的边AD的中点,且BE⊥AC交于点F,则下列结论中正确的是( )
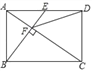
A. CF=3AF
B. △DCF是等边三角形
C. 图中与△AEF相似的三角形共有4个
D. tan∠CAD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的 A 、 B 两点所表示的数分别为 a 、b,a b 0 ,ab 0
![]()
(1)原点O 的位置在 ;
A.点 A 的右边 B. 点 B 的左边
C.点 A 与点 B 之间,且靠近点 A D. 点 A 与点 B 之间,且靠近点 B
(2)若 a b 2 ,
①利用数轴比较大小: a 1, b 1 ;(填“>”、“<”或“=”)
②化简:|a-1|+|b+1|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com