
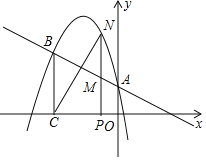
【题目】如图所示,二次函数y=ax2﹣![]() x+c的图象经过点A(0,1),B(﹣3,
x+c的图象经过点A(0,1),B(﹣3, ![]() ),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
(1)求直线AB的解析式和二次函数的解析式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)点N是二次函数图象上一点(点N在AB上方),是否存在点N,使得BM与NC相互垂直平分?若存在,求出所有满足条件的N点的坐标;若不存在,说明理由.
【答案】(1)y=﹣![]() x+1;y=﹣
x+1;y=﹣![]() x2﹣
x2﹣![]() x+1;(2)当m=﹣
x+1;(2)当m=﹣![]() 时,MN取最大值,最大值为
时,MN取最大值,最大值为![]() ;(3)存在点N,使得BM与NC相互垂直平分,点N的坐标为(﹣1,4)
;(3)存在点N,使得BM与NC相互垂直平分,点N的坐标为(﹣1,4)
【解析】试题分析:(1)根据已知点的坐标利用待定系数法即可得出结论;
(2)设点N的坐标为![]() 则点M的坐标为
则点M的坐标为
![]() 用含
用含![]() 的代数式表示出来
的代数式表示出来![]() ,结合二次函数的性质即可解决最值问题;
,结合二次函数的性质即可解决最值问题;
(3)假设存在,设点N的坐标为![]() 连接
连接![]() ,当四边形
,当四边形![]() 为菱形时,
为菱形时, ![]() 与
与![]() 相互垂直平分,根据
相互垂直平分,根据![]() 算出
算出![]() 的值,从而得出点
的值,从而得出点![]() 的坐标,再去验证
的坐标,再去验证![]() 是否等于
是否等于![]() ,由此即可得出结论.
,由此即可得出结论.
试题解析:(1)设直线AB的解析式为:y=kx+b,
∴
∴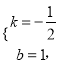
∴直线AB的解析式为: ![]()
把![]() 代入
代入![]() 得,
得, 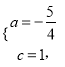
∴二次函数的解析式为: ![]()
(2)设点N的坐标为![]() 则点M的坐标为
则点M的坐标为
![]()
![]()
∴当![]() 时,MN取最大值,最大值为
时,MN取最大值,最大值为![]()
(3)假设存在,设点N的坐标为![]() 连接BN、CM,如图所示.
连接BN、CM,如图所示.
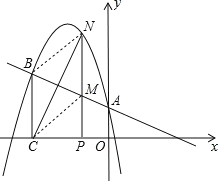
若要BM与NC相互垂直平分,只需四边形BCMN为菱形即可。
∵点B坐标为![]() 点C的坐标为(3,0),
点C的坐标为(3,0),
∴BC=52.
∵四边形BCMN为菱形,
![]() 解得:
解得: ![]()
当m=2时,点N的坐标为![]()
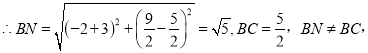
故m=2(舍去);
当m=1时,点N的坐标为(1,4),
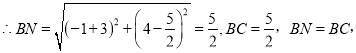
∴点N(1,4)符合题意.
故存在点N,使得BM与NC相互垂直平分,点N的坐标为(1,4).


科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上一点,C、D两点分别从P、B出发以1cm/s、2 cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置: ![]()
(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求![]() 的值。
的值。
![]()
(3)在(1)的条件下,若C、D运动5秒后,恰好有![]() ,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②![]() 的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点E在正方形![]() 的
的![]() 边上(不与点B,C重合),
边上(不与点B,C重合),![]() 是对角线,延长
是对角线,延长![]() 到点F,使
到点F,使![]() ,过点E作
,过点E作![]() 的垂线,垂足为G,连接
的垂线,垂足为G,连接![]() ,
,![]() .
.

(1)根据题意补全图形,并证明![]() ;
;
(2)①用等式表示线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
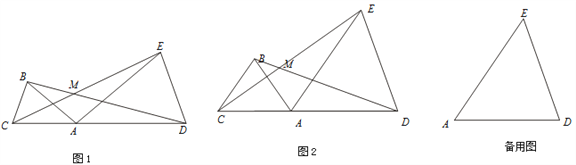
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
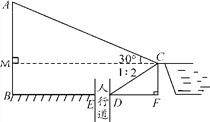
【题目】城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
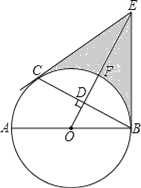
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数学运算”是数学学科核心素养之一,某校对七年级学生“数学运算能力”情况进行调研,从该校360名七年级学生中抽取了部分学生进行运算能力测试井进行分析,成绩分为A、B、C三个层次,绘制了频数分布表(如下),请根据图表信息解答下列问题:

(1)补全频数分布;
(2)如果成绩为A等级的同学属于优秀,请你估计该校七年级约有多少人达到优秀水平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC平分∠MON,P为OC上一点,PA⊥OM,PB⊥ON,垂足分别为A、B,连接AB,得到以下结论:(1)PA=PB;(2)OA=OB;(3)OP与AB互相垂直平分;(4)OP平分∠APB,正确的个数是( )
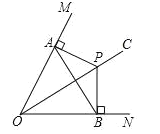
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
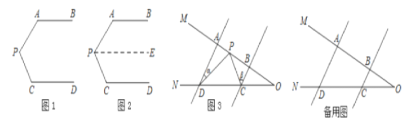
(1)天天同学看过图形后立即口答出:∠APC=110°,请你补全他的推理依据.
如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD.(___)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(___)
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(___)
问题迁移:
(2)如图3,AD∥BC,当点P在A. B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由。
(3)在(2)的条件下,如果点P在A. B两点外侧运动时(点P与点A. B. O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com