
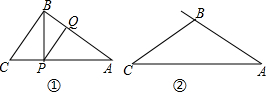
���� ��1����������ó���AQP�ס�BCP�������������ε����ʵó���A=��PBC�����ɡ�C=��C�����ɵó���BPC�ס�ABC��
��2���ɣ�1���ã���BPC�ס�ABC�������������ε����ʵó�$\frac{CP}{BC}=\frac{BC}{AC}$����CP=x��AP=BC=y����$\frac{x}{y}=\frac{y}{x+y}$�����x=$\frac{-1+\sqrt{5}}{2}$y���ó�$\frac{CP}{AP}=\frac{x}{y}$=$\frac{\sqrt{5}-1}{2}$���ɣ�
��3������B����CBP=��A��BP��AC�ڵ�P������P����QPA=��BPC��PQ��AB���ӳ������ڵ�Q����P��Q��Ϊ����ĵ㣻�ó���AQP�ס�BCP�ס�ACB���ó���Ӧ�߳ɱ���$\frac{CP}{BC}=\frac{BC}{AC}$��$\frac{AP}{AB}=\frac{AQ}{AC}$���������CP��AQ�����ɵó�BQ�ij���
��� ��1���⣻��BPC�ס�ABC���������£�
�ߡ�ABC�У���P��QΪAC��AB���ϵ�һ�ԡ����Ƶ㡱��
���AQP�ס�BCP��
���A=��PBC��
�֡ߡ�C=��C��
���BPC�ס�ABC��
��2��֤�����ɣ�1���ã���BPC�ס�ABC��
��$\frac{CP}{BC}=\frac{BC}{AC}$��
��CP=x��AP=BC=y��
��$\frac{x}{y}=\frac{y}{x+y}$��
��ã�x=$\frac{-1��\sqrt{5}}{2}y$����ֵ��ȥ����
��x=$\frac{-1+\sqrt{5}}{2}$y��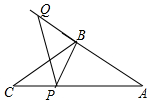
��$\frac{CP}{AP}=\frac{x}{y}$=$\frac{\sqrt{5}-1}{2}$��
���PΪ�߶�AC�Ļƽ�ָ�㣨��CP=$\frac{\sqrt{5}-1}{2}$AP����
��3���⣺����B����CBP=��A��BP��AC�ڵ�P������P����QPA=��BPC��PQ��AB���ӳ������ڵ�Q��
��P��Q��Ϊ����ĵ㣻
��ͼ��ʾ��
��������ã���AQP�ס�BCP�ס�ACB��
��$\frac{CP}{BC}=\frac{BC}{AC}$��$\frac{AP}{AB}=\frac{AQ}{AC}$��
��$\frac{CP}{12}=\frac{12}{18}$��$\frac{18-CP}{12}=\frac{AQ}{18}$��
��ã�CP=8��AQ=15��
��BQ=AQ-AB=15-12=3��
���� �������������ۺ���Ŀ���������¶��塰���Ƶ㡱�����������ε��ж������ʡ��ƽ�ָ���֪ʶ�����������¶�������������ε��ж��������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7��b��8 | B�� | 7��b��8 | C�� | 8��b��9 | D�� | 8��b��9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-y����-y-x��=y2-x2 | B�� | ��2x-y����y-2x��=-y2-4x2 | ||
| C�� | ��2a-1��2=4a2-2a+1 | D�� | ��3-x��2=9-x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
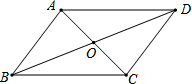 ��ͼ��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O������˵��һ����ȷ���ǣ�������
��ͼ��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O������˵��һ����ȷ���ǣ�������| A�� | AO=BO | B�� | AC��BD | C�� | AB=BC | D�� | AB=CD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y��ֵΪ�� | |
| B�� | ˫������һ�������� | |
| C�� | y��x����������� | |
| D�� | �����ڵ�ÿһ�����ޣ�y��x����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 17a3b6 | B�� | 8a6b12 | C�� | -a3b6 | D�� | 15a3b6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ���a+c��b����4ac��b2����2a+b��0��������ȷ���У�������
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ���a+c��b����4ac��b2����2a+b��0��������ȷ���У�������| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ֱ����ֱ�߶Ͽ�����λ����E��D��B��F��ͬһֱ���ϣ�����ADE=135�㣬���DBC�Ķ����ǣ�������
��ͼ����ֱ����ֱ�߶Ͽ�����λ����E��D��B��F��ͬһֱ���ϣ�����ADE=135�㣬���DBC�Ķ����ǣ�������| A�� | 65�� | B�� | 55�� | C�� | 45�� | D�� | 35�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com