
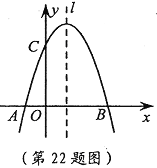
【题目】(本题10分)如图,已知抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴![]() 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。
【答案】(1)m=2,(1,4);(2)(1,2).
【解析】
试题分析:(1)把点B的坐标为(3,0)代入![]() ,解方程即可得m的值,求出m的值后把抛物线化为顶点式即可得抛物线的顶点坐标;(2)连接BC交抛物线的对称轴于点P,此时PA+PC的值最小,利用待定系数法求得直线BC的解析式,再求点P的坐标即可.
,解方程即可得m的值,求出m的值后把抛物线化为顶点式即可得抛物线的顶点坐标;(2)连接BC交抛物线的对称轴于点P,此时PA+PC的值最小,利用待定系数法求得直线BC的解析式,再求点P的坐标即可.
试题解析:(1)把点B的坐标为(3,0)代入得:![]() ,
,
解得m=2,
∴![]()
∵![]()
∴顶点坐标为(1,4).
(2)连接BC交抛物线的对称轴l于点P,此时PA+PC的值最小,
设Q是直线l上任意一点,连结AQ,CQ,BQ,
∵直线L垂直平分AB,
∴AQ=BQ,AP=BP,
∴AQ+CQ=BQ+CQ≥BC,
BC=BP+CP=AP+CP,
即AQ+CQ≥AP+CP
设直线BC的解析式为y=kx+b(k≠0),
把(3,0),(0,3)代入得,
![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=-x+3,
当x=1时,y=-1+3=2.
答:当PA+PC的值最小时,点P的坐标为(1,2).



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的面积为128cm2 , 它的两条对角线交于点O1 , 以AB、AO1为两边邻作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB、AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABC7O7的面积为 . 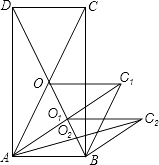
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农民张大伯因病住院,手术费为a元,其它费用为b元.由于参加农村合作医疗,
手术费报销85%,其它费用报销60%,则张大伯此次住院可报销 ▲ 元.(用代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC与G,∠E=∠1,求证:AD平分∠BAC. 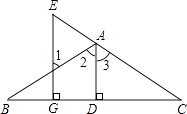
证明:∵AD⊥BC于D,EG⊥BC于G()
∴∠ADC=90°,∠EGC=90°()
∴∠ADC=∠EGC
∴AD∥EG()
∴∠1=∠2()
∠E=∠3()
又∵∠E=∠1()
∴∠2=∠3
∴AD平分∠BAC().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B旋转90°,分别得到线段B P1,B P2,称点P1,P2为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图.
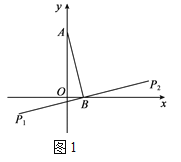
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(-2,0)时,点A关于点B的“伴随点”的坐标分别为 ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
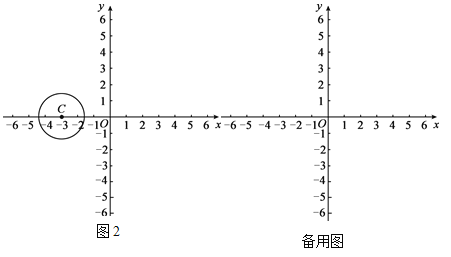
(2)如图2,点C的坐标为(-3,0),以C为圆心, ![]() 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物深度![]() (微克/毫升)与服药时间
(微克/毫升)与服药时间![]() 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当![]() 时,
时,![]() 与
与![]() 成反比).
成反比).

(1)根据图象分别求出血液中药物浓度上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com