
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.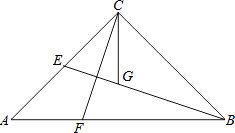
(1)求证:CF=BG;
(2)延长CG交AB于点H,判断点G是否在线段AB的垂直平分线上?并说明理由.
(3)过点A作AD⊥AB交BE的延长线于点D,请证明:CF=2DE.
【答案】
(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∵CG平分∠ACB,
∴∠BCG=45°=∠A,
∴∠BCG=∠CAB=45°,
在△ACF和△BCG中,  ,
,
∴△ACF≌△BCG(ASA),
∴AF=CG,CF=BG
(2)解:点G在线段AB的垂直平分线上,如图1所示:理由如下:

∵AC=BC,CG平分∠ACB,
∴CH⊥AB,H为AB中点,
∴点G在线段AB的垂直平分线上
(3)证明:连接AG.如图2所示:

由(2)可知,AG=BG,∠GAB=∠GBA,
∵AD⊥AB,
∴∠GAB+∠GAD=∠GBA+∠D=90°,
∴∠GAD=∠D,
∴GA=GD=GB=CF.
∵AD⊥AB,CH⊥AB
∴CH∥AD,
∴∠D=∠EGC,
∵E为AC中点,
∴AE=EC,
在△AED和△CEG中,  ,
,
∴△AED≌△CEG(SAS),
∴DE=EG,
∴DG=2DE,
∴CF=2DE
【解析】 (1)根据等腰直角三角形的性质及角平分线的定义得出∠BCG=∠CAB=45°,然后由ASA判断出△ACF≌△BCG,然后根据全等三角形的性质得出结论;
(2)根据等腰三角形的三线合一得出CH⊥AB,H为AB中点,故点G在线段AB的垂直平分线上;
(3)连接AG,由垂直的定义得出∠GAD=∠D, 根据等边对等角得出GA=GD=GB=CF,由平行线的判定得出CH∥AD,故∠D=∠EGC,然后由SAS得出△AED≌△CEG,根据全等三角形的性质得出结论。
【考点精析】根据题目的已知条件,利用平行线的判定与性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
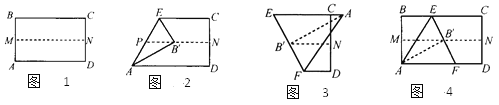
【题目】取一张矩形纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B',得Rt△AB'E,如图2;第三步:沿EB'线折叠得折痕EF,使A点落在EC的延长线上,如图3.
利用展开图4探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
(1)求抛物线的解析式;
(2)若PA:PB=3:1,求一次函数的解析式;
(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个球,其中7个黄球,8个黑球,5个红球,这些球只有颜色不同,其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2011年5月1日﹣10日十天的空气污染指数的数据如下(主要污染物为可吸入颗粒物):61,75,70,56,81,91,92,91,75,81.那么该组数据的极差和中位数分别是( )
A. 36,78 B. 36,86 C. 20,78 D. 20,77.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )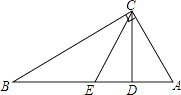
A.60°
B.45°
C.30°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列现象:①电梯的升降运动;②飞机在地面上沿直线滑行;③风车的转动;④钟摆的摆动.其中属于平移的是( )
A. ①③B. ①②C. ②③D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】政府为了更好地加强城市建设,就社会热点问题广泛征求市民意见,调查方式是发调查表,要求每位被调查人员只写一个你最关心的有关城市建设的问题,经统计整理,发现对环境保护问题提出的最多,有700人,同时作出相应的条形统计图,如图所示,请回答下列问题.
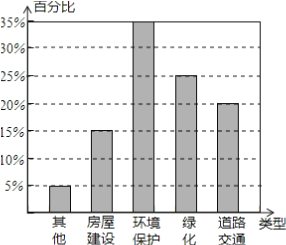
(1)共收回调查表 张;
(2)提道路交通问题的有 人;
(3)请你把这个条形统计图用扇形统计图表示出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com