
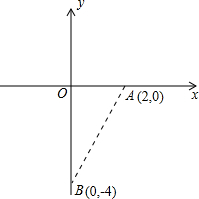 在直角坐标系中,以点A(2,0)为圆心作圆,使圆经过点B(0,-4),如图所示,试判断C(0,4)、D(-2,0)、E(0,8)与⊙A的位置关系.若点M(0,m)在⊙A外,求m的取值范围.
在直角坐标系中,以点A(2,0)为圆心作圆,使圆经过点B(0,-4),如图所示,试判断C(0,4)、D(-2,0)、E(0,8)与⊙A的位置关系.若点M(0,m)在⊙A外,求m的取值范围.  高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,AB=CB,∠ABC=90°,∠CAB=∠ACB,F为AB延长线上一点,点E在BC上,且∠EAB=∠FCB.
如图所示,在△ABC中,AB=CB,∠ABC=90°,∠CAB=∠ACB,F为AB延长线上一点,点E在BC上,且∠EAB=∠FCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
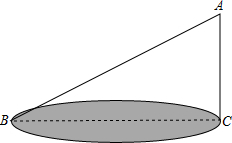 公园有三个景点A、B、C构成如图所示的直角三角形,由于B、C两景点之间有一山相隔,为方便游客,准备在B、C间挖条隧道.已知∠ACB=90°,AB=3千米,AC=2千米.试用计算器探索:这条隧道至少要修多少米?(精确到1米)
公园有三个景点A、B、C构成如图所示的直角三角形,由于B、C两景点之间有一山相隔,为方便游客,准备在B、C间挖条隧道.已知∠ACB=90°,AB=3千米,AC=2千米.试用计算器探索:这条隧道至少要修多少米?(精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
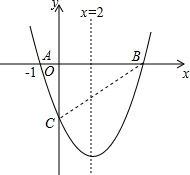 如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0),其顶点为D.
如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0),其顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com