
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?

科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC; 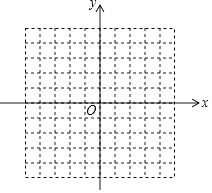
(2)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标;
(3)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E,F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,∠EAF=90°,BC=12,EF=5.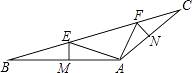
(1)求∠BAC的度数;
(2)求S△EAF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,我市自来水公司对水价作出规定:当每月用水量不超过5t时,每吨收费1.8元;当超过5t时,超过部分每吨收费3元.某个月一户居民交水费36元,问这户居民这个月用水多少t?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求画图.
(1)如图(1)所示,过点A画MN∥BC;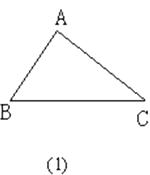
(2)如图(2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;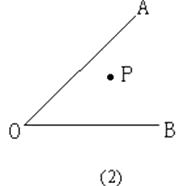
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.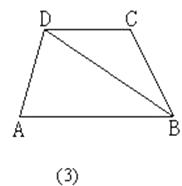
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠a.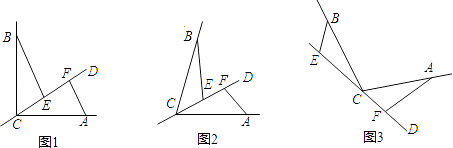
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图l,若∠BCA=90°,∠a=90°,则BECF;EF|BE﹣AF|(填“>”,“<”或“=”);
②如图(2),若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 , 使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com