
分析 (1)根据负整数指数幂以及零指数幂先化简各式,然后进行加减运算;
(2)先进行幂的乘方运算,然后进行单项式乘除运算,最后合并同类项即可;
(3)根据多项式除以单项式运算法则计算即可;
(4)多次利用平方差公式计算即可;
(5)利用平方差公式和完全平方公式去掉括号,然后合并同类项即可;
(6)把(x+y)看成一个整体,利用平方差公式进行计算.
解答 解:(1)原式=1+4-1=4;
(2)原式=4x6y2•(-2xy)+(-8x9y3)•$\frac{1}{2{x}^{2}}$
=-8x7y3-4x7y3
=-12x7y3;
(3)原式=[3m2(2n-2n2-1)]÷(-3m2)
=-2n+2n2+1
=2n2-2n+1;
(4)原式=(1-x2)(1+x2)(1+x4)
=(1-x4)(1+x4)
=1-x8;
(5)原式=4x2-y2+x2+2xy+y2-4x2+2xy
=x2+4xy;
(6)原式=(x+y)2-z2
=x2+y2-z2+2xy.
点评 本题主要考查了整式的混合运算的知识,解答本题的关键是掌握平方差公式以及完全平方公式以及幂的乘方运算等知识,此题难度不大.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
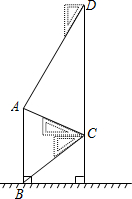 如图,中医药大学想把原来的校园内出现裂痕的李时珍的雕塑重新建造,为了和原来的高度一致,雕塑师小李为了测量其高度在教学楼二楼找到一点C,利用三角板测的雕塑顶端A点的仰角为30°,底部B点的俯角为45°,又在五楼找到一点D,利用三角板测得A点的俯角为60°.若CD为10米,求雕塑AB的高度(结果保留一位小数,$\sqrt{3}≈1.73$).
如图,中医药大学想把原来的校园内出现裂痕的李时珍的雕塑重新建造,为了和原来的高度一致,雕塑师小李为了测量其高度在教学楼二楼找到一点C,利用三角板测的雕塑顶端A点的仰角为30°,底部B点的俯角为45°,又在五楼找到一点D,利用三角板测得A点的俯角为60°.若CD为10米,求雕塑AB的高度(结果保留一位小数,$\sqrt{3}≈1.73$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com