
 是正方形,点
是正方形,点 在
在 上,
上, ,垂足为
,垂足为 ,请你在
,请你在 上确定一点
上确定一点 ,使
,使
 ,请你写出两种确定点G的方案,并写出其中一种方案的具体作法和证明
,请你写出两种确定点G的方案,并写出其中一种方案的具体作法和证明 .
.
|
 ;方案
;方案
|
|
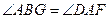 交AE于点G;…………………………2分
交AE于点G;…………………………2分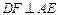 ,BG⊥AE,
,BG⊥AE,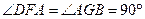 .…………
.………… …………………………………………………4分
…………………………………………………4分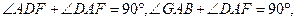
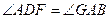 .……………………………………………………………………5分
.……………………………………………………………………5分 是正方形,∴AD=AB,
是正方形,∴AD=AB, 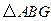 与
与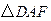 中,
中,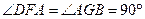 ,
,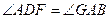 ,AD=AB,
,AD=AB, (AAS). ………………………………………………………6分
(AAS). ………………………………………………………6分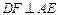 ,AD⊥AE,
,AD⊥AE,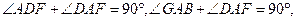
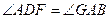 .……………………………………………………………………4分
.……………………………………………………………………4分 是正方形,∴AD=AB, …
是正方形,∴AD=AB, … …………………………………………5分
…………………………………………5分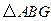 与
与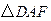 中,AG=DF,
中,AG=DF,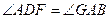 ,AD=AB,
,AD=AB, (SAS). ………………………………………………………6分
(SAS). ………………………………………………………6分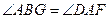 交AE于点G,证明如下:
交AE于点G,证明如下: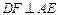 ,AD⊥AE,
,AD⊥AE,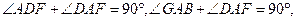
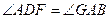 .……………………………………………………………………4分
.……………………………………………………………………4分 是正方形,∴AD=AB, ……………………………………………5分
是正方形,∴AD=AB, ……………………………………………5分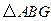 与
与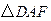 中,
中,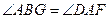 , AD=AB,
, AD=AB,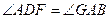
 (ASA). ………………………………………………………6分
(ASA). ………………………………………………………6分

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 状并证明;
状并证明; B,求证:梯形ABCD是等腰梯形.
B,求证:梯形ABCD是等腰梯形.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,求三角形DBF的面积.
,求三角形DBF的面积. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 =
= ,求证:
,求证: .
.

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com