
【题目】在△ABC中,∠A=40°.
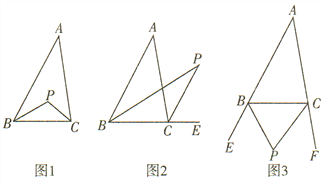
(1)如图1,若两内角∠ABC,∠ACB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(2)如图2,若内角∠ABC,外角∠ACE的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(3)如图3,若两外角∠EBC,∠FCB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 .
(选择其中一种数量关系加以证明)
【答案】(1)∠P=90°+![]() ∠A;(2)∠P=
∠A;(2)∠P=![]() ∠A;(3)70°;∠P=90°-∠A.
∠A;(3)70°;∠P=90°-∠A.
【解析】试题分析:(1)根据三角形内角和定理求出∠B和∠C,再根据角平分线的性质和三角形内角和是180°求出∠P=180°-![]() (∠B+∠C);
(∠B+∠C);
(2)根据三角形的一个外角等于和它不相邻的两个内角的和以及叫平分线的性质可求出∠P,可得∠A与∠P之间的数量关系;
(3)根据三角形的一个外角等于和它不相邻的两个内角的和求得:∠EBC+∠BCF=∠A+∠ACB+∠ABC+∠A=180°+∠A,在△BCP中根据角平分线的定义以及三角形内角和定理即可求解.
试题解析:(1)∠ABC+∠C=180°∠A=180°40°=140°
∴![]() (∠ABC+∠C)=
(∠ABC+∠C)=![]() ×140°=70°,
×140°=70°,
∴∠P=180°![]() (∠ABC+∠C)=110°.
(∠ABC+∠C)=110°.
∠A与∠P之间的数量关系是∠P=90°+![]() ∠A;
∠A;
(2)∵![]() ∠ACE=
∠ACE=![]() ∠ABC+∠P,
∠ABC+∠P,
∴![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() ∠ABC+∠P,
∠ABC+∠P,
∴![]() (40°+∠ABC)=
(40°+∠ABC)=![]() ∠ABC+∠P,
∠ABC+∠P,
∴∠P=20°.
∠A与∠P之间的数量关系是∠P=![]() ∠A;
∠A;
(3)∵∠EBC=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴∠EBC+∠BCF=∠A+∠ACB+∠ABC+∠A=180°+∠A,
∴∠PBC+∠PCB=90°+![]() ∠A.
∠A.
又∵∠PBC+∠PCB+∠P=180°,
∴90°+![]() ∠A+∠P=180°,即∠P=90°
∠A+∠P=180°,即∠P=90°![]() ∠A,
∠A,
当∠A=40°时,∠P=70°.


科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个,这些球除颜色外都相同,求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是是红球;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(18分)计算与化简:
⑴ -3-(-9)+5
⑵ (1-![]() +
+![]() )×(-48)
)×(-48)
⑶16÷(-2)3-(-![]() )×(-4)
)×(-4)
⑷-12-(-10)÷![]() ×2+(-4)2
×2+(-4)2
⑸ -23-(2-1.5)÷![]() ×∣-6-(-3)2∣
×∣-6-(-3)2∣
⑹-9a2+[2a2-2(a-3a2)+5a]
查看答案和解析>>
科目:初中数学 来源: 题型:
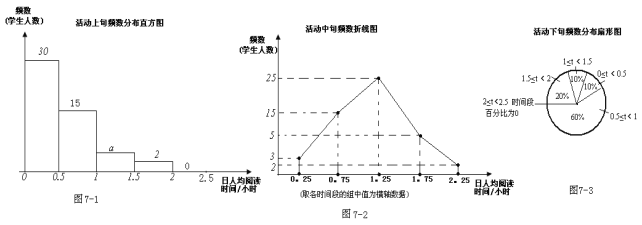
【题目】以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、下旬)日人均阅读时间的情况:
(1)从以上统计图可知,九年级(1)班共有学生 人;
(2)图7-1中a的值是 ;
(3)从图7-1、7-2中判断,在这次读书月活动中,该班学生每日阅读时间 (填“普遍增加了”或“普遍减少了”);
(4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图的变化趋势,至读书月活动结束时,该班学生日人均阅读时间在0.5~1小时的人数比活动开展初期增加了 人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖家开了甲、乙两个超市,两个超市在3月份的销售额均为a万元,在4月份和5月份这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%.
(1)5月份甲超市的销售额比乙超市多多少?
(2)如果a=250,x=2,那么5月份甲超市的销售额比乙超市多多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com