
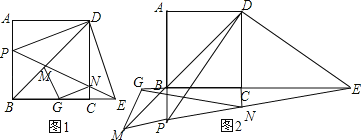
【题目】在正方形ABCD中,BD为对角线,点P从A出发,沿射线AB运动,连接PD,过点D作DE⊥PD,交直线BC于点E.

(1)当点P在线段AB上时(如图1),求证:BP+CE=![]() BD;
BD;
(2)当点P在线段AB的延长线上时(如图2),猜想线段BP、CE、BD之间满足的关系式,并加以证明;
(3)若直线PE分别交直线BD、CD于点M、N,PM=3,EN=4,求PD的长.
【答案】(1)证明见解析(2)CE﹣BP=![]() BD,理由见解析(3)3
BD,理由见解析(3)3![]() 或6
或6![]()
【解析】
试题分析:(1)根据已知和图形证明△PAD≌△ECD,得到AP=CE,根据AB=![]() BD,得到答案;
BD,得到答案;
(2)与(1)的方法类似,求出结论;
(3)分P在线段AB上和P在AB延长线上两种情况进行讨论,根据三角形全等和勾股定理证明结论.
证明:(1)∵四边形ABCD是正方形,
∴∠A=∠ADC=∠BCD=∠DCE=90°,AD=CD,
∵DE⊥PD,
∴∠ADC=∠PDE=90°,
∴∠ADP=90°﹣∠PDC=∠CDE,
∴△PAD≌△ECD,
∴AP=CE,
∴BP+CE=BP+AP=AB=![]() BD;
BD;
(2)CE﹣BP=![]() BD;
BD;
理由:△PAD≌△ECD,
∴CE=AP,
∴CE﹣BP=AP﹣BP=AB=![]() BD;
BD;
(3)①当P在线段AB上时,
如图1所示,在BC上取一点G使得BG=BP,连接MG、NG,
∵△APD≌△CED,
∵AP=CE,PD=ED,
∴△PED是等腰直角三角形,
∴AB=BC=AP+BP=BG+CG,
∴CG=CE,
∴可证△NCG≌△NCE,
∴NG=NE,∠NGC=∠NEC,
∵∠PBM=∠GBM=45°,BP=BG,BM=BM,
∴△BPM≌△BGM
∴PM=GM,∠MGB=∠MPB,
又∠NEC+∠MPB=90°,
∴∠NGC+∠MGB=90°,
∴∠MGN=90°,
∴MN=![]() =5,
=5,
∴PE=PM+MN+EN=3+5+4=12,
∴PD=![]() PE=6
PE=6![]() ;
;
②当P在AB延长线上时,
如图2所示,延长CB至G,使得CG=CE,连接MG、NG,
∵AP=CE,
∴CE﹣BC=CG﹣BC=AP﹣AB=BP=BG,
同①可证△△BMG≌△BMP,△CNG≌△CNE,
∴PM=GM,GN=EN,∠BGM=∠BPM=90°+∠CEN=90°+CGN,
∴∠CGN=∠BGM﹣90°=∠BGM﹣∠MGN,
∴∠MGN=90°,
∴MN=![]() =5,
=5,
∴PN=MN﹣PM=5﹣3=2,
∴PE=PN+EN=2+4=6,
∴PD=![]() PE=3
PE=3![]() ,
,
∴PD的长为3![]() 或6
或6![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为![]() ,按表格要求确定奖项.
,按表格要求确定奖项.

(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD垂直于弦AB,垂足为E,AM⊥BC于点M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=![]() ,ON=1,求⊙O的半径;
,ON=1,求⊙O的半径;
(3)若![]() 且AE=4,求CM的长
且AE=4,求CM的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | b | 1 | 0 | 1 | 2 | … |
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .

查看答案和解析>>
科目:初中数学 来源: 题型:
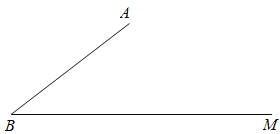
【题目】如图,已知∠ABM=30°,AB=20,C是射线BM上一点.
(1)在下列条件中,可以唯一确定BC长的是 ;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=![]() ;③△ABC的面积为126.
;③△ABC的面积为126.
(2)在(1)的答案中,选择一个作为条件,画出示意图,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
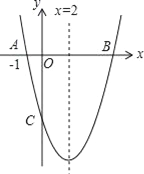
【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com