练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的度数是（　　）

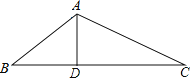
    A. 20°B. 30°C. 45°D. 60°

    【答案】A

    【解析】

    在DC上取DE=DB．连接AE，在Rt△ABD和Rt△AED中，BD=ED，AD=AD．证明△ABD≌△AED即可求解．

    如图，

    在DC上取DE=DB，连接AE．

    在Rt△ABD和Rt△AED中，

    ，

    ∴△ABD≌△AED（HL）．

    ∴AB=AE，∠B=∠AED．

    又∵AB+BD=CD

    ∴EC=CD-DE=CD-BD=（AB+BD）-BD=AB=AE，

    即EC=AE，

    ∴∠C=∠CAE

    ∴∠B=∠AED=2∠C

    又∵∠B+∠C=180°-∠BAC=60°

    ∴∠C=20°，

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠ADC=∠ABC=90°，与∠ADC、∠ABC相邻的两外角平分线交于点E，若∠A=50°,则∠E的度数为( )

    A. 60°B. 50°C. 40°D. 30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)观察下列各式： ……

    你发现了什么规律？试用你发现的规律填空：

    ；

    (2)请你用含一个字母的等式将上面各式呈现的规律表示出来，并用所学数学知识说明你所写式子的正确性.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为（ ）

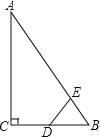
    A．2B．2.5或3.5

    C．3.5或4.5D．2或3.5或4.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

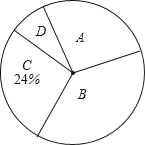
    【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为A、B、C、D四类．其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表：

    类别

    A

    B

    C

    D

    频数

    30

    40

    24

    b

    频率

    a

    0.4

    0.24

    0.06

    （1）表中的a=　 　，b=　 　；

    （2）根据表中数据，求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数；

    （3）若该校有学生1000名，根据调查结果估计该校学生中类别为C的人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

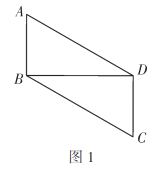
    图形变换的基本方式有:平移变换、旋转变换、轴对称变换.在数学综合与实践课上，张老师将两块含角的全等三角尺按图1方式摆放在一起 ，其中.同时，要求班内各小组对图形进--步操作变换并提出问题，请你帮各小组进行解答.

    [独立思考]

    （1）张老师首先提出问题:图1中，四边形是平行四边形吗？说明理由；

    [提出问题]

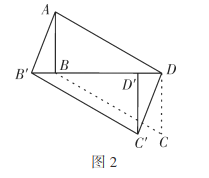
    （2）如图2，“励志”小组将沿射线方向平移到的位置，分别连接，进一步提出问题：四边形是平行四边形吗？说明理由；

    [拓展延伸]

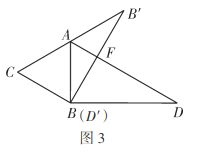
    （3）“慎密”小组提出的问题是：如图3，两个全等的三角尺重叠放在的位置，将其中一个三角尺绕着点按逆时针方向旋转至的位置，使点恰好落在边上，与相交于点，若，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD中，∠DAB＝30°，AB＝6，BC＝2，P为边CD上的一动点，则2PB+ PD的最小值等于______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

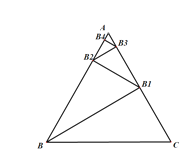
    【题目】如图，△ABC是一个边长为1的等边三角形，BB1是△ABC的高，B1B2是△ABB1的高，B2B3是△AB1B2的高，……Bn-1Bn是△ABn-2Bn-1的高，则B4B5的长是________，猜想Bn-1Bn的长是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形的边、在坐标轴上，点坐标，将正方形绕点顺时针旋转角度，得到正方形，交线段于点，的延长线交线段于点，连、．

    （1）求证：；

    （2）求的度数，并判断线段、、之间的数量关系，说明理由；

    （3）当时，求直线的解析式．

    查看答案和解析>>

    同步练习册答案