
分析 (1)根据绝对值的性质、零指数幂的性质、负指数幂的性质、特殊角的三角函数值以及二次根式的化简的知识,即可将原式化简,继而求得答案;
(2)先利用分式的混合运算法则化简,再代入数值求解即可.
解答 解:(1)$|{\sqrt{3}-2}|+{(π-2012)^0}-{({-\frac{1}{3}})^{-1}}-3tan30°+\sqrt{12}$
=2-$\sqrt{3}$+1+3-3$\sqrt{3}$+2$\sqrt{3}$
=6-2$\sqrt{3}$;
(2)原式=[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]•$\frac{x(x+2)(x-2)}{x+2}$
=$\frac{(x+2)(x-2)-x(x-1)}{x(x-2)^{2}}$•x(x-2)
=$\frac{{x}^{2}-4-{x}^{2}+x}{x(x-2)^{2}}$•x(x-2)
=$\frac{x-4}{x-2}$,
∵x≠0,x≠±2,
∴当x=5时,原式=$\frac{5-4}{5-2}$=$\frac{1}{3}$.
点评 此题考查了分式的混合运算、绝对值的性质、零指数幂的性质、负指数幂的性质、特殊角的三角函数值以及二次根式的化简.注意熟记各性质是关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
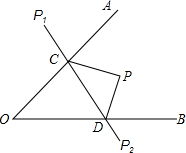 如图所示,P是∠A0B内任一点,以OA、OB为对称轴分别画出点P经轴对称变换后的点P1、P2,连结P1P2,分别与OA、OB相交于点C、D,若P1P2=8cm,求△PCD的周长.
如图所示,P是∠A0B内任一点,以OA、OB为对称轴分别画出点P经轴对称变换后的点P1、P2,连结P1P2,分别与OA、OB相交于点C、D,若P1P2=8cm,求△PCD的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com