
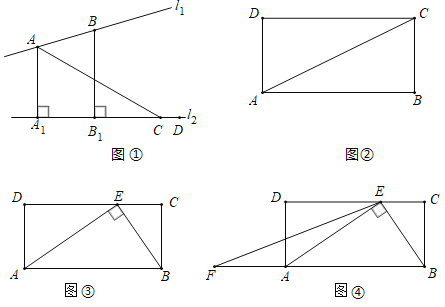
【题目】如图①,平面内的两条直线![]() 点
点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,过
上,过![]() 两点分别作
两点分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,我们把线段
,我们把线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的正投影,其长度可记为
上的正投影,其长度可记为![]() 或
或![]() 特别地,线段
特别地,线段![]() 在直线
在直线![]() 上的正投影就是线段
上的正投影就是线段![]() .请依据上述定义解决如下问题:
.请依据上述定义解决如下问题:
(1)如图①,若![]() ,则
,则![]() .
.
(2)如图②,在矩形![]() 中,
中,![]() ,
,![]() ,则
,则![]() .
.
(3)如图③,在矩形![]() 中,点
中,点![]() 在
在![]() 边上(
边上(![]() ),连接
),连接![]() 、
、![]() ,
,![]()
①若![]() ,求矩形
,求矩形![]() 的面积.
的面积.
②如图④,点![]() 在
在![]() 延长线上,连按
延长线上,连按![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() .
.
【答案】(1)5;(2) ![]() ;(3) ①
;(3) ①![]() ;②
;②![]() .
.
【解析】
(1)由题意即可得出结果;
(2)过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,由四边形
,由四边形![]() 是矩形,
是矩形, ![]() ,
,![]() ,得出
,得出![]() ,
,![]() ,由勾股定理得出
,由勾股定理得出![]() ,证明
,证明![]() ,得出
,得出![]() ,求出
,求出![]() ,即可得出结果;
,即可得出结果;
(3)①过点![]() 作
作![]() 于
于![]() ,由
,由![]() ,求出
,求出![]() ,证明
,证明![]() ,求出
,求出![]() ,则
,则![]() ;
;
②过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,由
,由![]() ,
,![]() ,得出
,得出![]() ,
,![]() ,由
,由![]() ,求出
,求出![]() ,再由勾股定理得出
,再由勾股定理得出![]() ,
,![]() ,证明
,证明![]() ,求出
,求出![]() ,再由勾股定理得出
,再由勾股定理得出![]() ,即可得出结果.
,即可得出结果.
解:(1)∵![]() ,
,
∴![]() ,
,
故答案为:5;
(2) 过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,如图②所示:
,如图②所示:
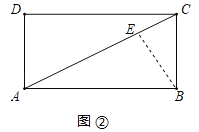
∵四边形![]() 是矩形,
是矩形, ![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(3)①过点![]() 作
作![]() 于
于![]() ,如图③所示:
,如图③所示:
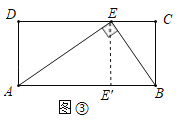
则四边形![]() 是矩形、四边形
是矩形、四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,如图④所示:
,如图④所示:
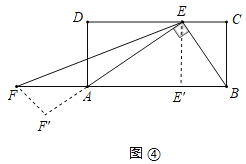
则四边形![]() 是矩形、四边形
是矩形、四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
由1得:![]() ,
,
∴![]() ,
,
即:![]() ,
,
解得:![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ,不合题意舍去,
,不合题意舍去,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某超市准备进一批每个进价为40元的小家电,经市场调查预测,售价定为50元时可售出400个;定价每增加1元,销售量将减少10个.
(1)设每个定价增加x元,此时的销售量是多少?(用含x的代数式表示)
(2)超市若准备获得利润6000元,并且使进货量较少,则每个应定价为多少元?
(3)超市若要获得最大利润,则每个应定价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片的烂泥湿地,为了人员和设备安全迅速地通过这片湿地,他们沿着前进路线铺了若干块大小不同的木板,构筑成一条临时通道,已知当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
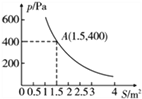
(1)请直接写出p与S 之间的关系式和自变量S 的取值范围;
(2)当木板面积为0.2 m2时,压强是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
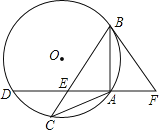
【题目】已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
(1)求证:BF与⊙O相切.
(2)若BF=5,cosC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
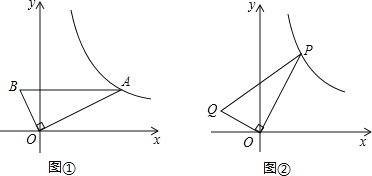
【题目】如图①,直角三角形AOB中,∠AOB=90°,AB平行于x轴,OA=2OB,AB=5,反比例函数的图象经过点A.
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过O 作OQ⊥OP,且OP=2OQ,连接PQ.设Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);
②运动服的进价是 元/件;当售价是 元/件时,月销利润最大,最大利润是 元.
(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com