
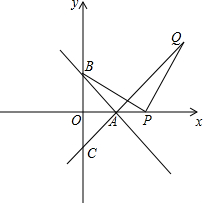
 直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.分析 (1)求出A、C两点坐标,利用待定系数法即可解决问题.
(2)结论:PB=PQ.由△ABG∽△PQG,推出$\frac{BG}{GQ}$=$\frac{AG}{PG}$,推出$\frac{BG}{AG}$=$\frac{GQ}{PG}$,因为∠BGQ=∠AGP,推出△BGQ∽△AGP,推出∠QBG=∠GAP=45°,由此即可解决问题.
(3)如图2中,$\frac{(MQ-AC)}{PM}$的值是定值,定值为1.作PG⊥PA交PA的延长线于G.首先证明四边形AMPG是正方形,再证明△PMQ≌△PGB,推出MQ=BG,由此即可解决问题.
解答 解:(1)∵直线y=-x+2与X轴、y轴交于A、B两点,
∴A(2,0),B(0,2),
∵OC=OB,
∴点C坐标(0,-2),
设直线AC的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=-2}\\{2k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴直线AC的解析式为y=x-2.
(2)如图1中,结论:PB=PQ.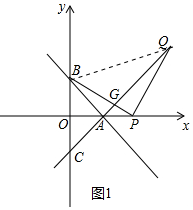
理由:连接BQ,AQ与PB交于点G.
∵OA=OB=OC,
∴∠OAB=∠OBA=∠OAC=∠OCA=45°,
∴∠CAB=∠BAQ=90°,
∵PB⊥PQ,
∴∠BAG=∠QPG=90°,
∵∠AGB=∠PGQ,
∴△ABG∽△PQG,
∴$\frac{BG}{GQ}$=$\frac{AG}{PG}$,
∴$\frac{BG}{AG}$=$\frac{GQ}{PG}$,∵∠BGQ=∠AGP,
∴△BGQ∽△AGP,
∴∠QBG=∠GAP,
∵∠OAC=∠PAG=45°,
∴∠PBQ=∠PAG=45°,∵∠BPQ=90°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ.
(3)如图2中,$\frac{(MQ-AC)}{PM}$的值是定值,定值为1.
理由:作PG⊥PA交PA的延长线于G.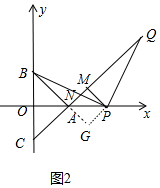
由(2)可知,∠PAM=∠PAG=45°,
∵PM⊥AQ,PG⊥AG,
∴PM=PG,
∵∠G=∠GAM=∠PMA=90°,
∴四边形AMPG是矩形,
∵PM=PG,
∴四边形AMPG是正方形,
∴AG=PM,
在△PMQ和△PGB中,
$\left\{\begin{array}{l}{∠Q=∠PBG}\\{∠PMQ=∠G}\\{PM=PG}\end{array}\right.$,
∴△PMQ≌△PGB,
∴MQ=BG,
∵AB=AC,
∴$\frac{MQ-AC}{PM}$=$\frac{BG-AB}{PM}$=$\frac{AG}{PM}$=1.
点评 本题考查一次函数综合题、等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考压轴题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
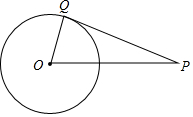 如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切
如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com