
 已知点A(-1,0),点B(4,0),点C在y轴的正半轴上,且∠ACB=90°.抛物线y=ax2+bx+c经过A、B、C三点,且顶点为M.
已知点A(-1,0),点B(4,0),点C在y轴的正半轴上,且∠ACB=90°.抛物线y=ax2+bx+c经过A、B、C三点,且顶点为M.分析 (1)由△AOC∽△COB可求得OC的长,可求得C点坐标,利用待定系数法可求得抛物线解析式;
(2)当AB为对角线时,由A、B关于对称轴对称可知,AB为平行四边形的对角线,可知满足条件的D点坐标抛物线的顶点,利用(1)中所求抛物线解析式可求得D点坐标;当AB为边时,则可知AB=HD,设出D点坐标,则可得到关于D点坐标的方程,可求得D点坐标;
(3)过N作NM∥y轴,交BC于点M,由B、C坐标可求得直线BC的解析式,设出N点坐标,则可表示出M点坐标,从而可表示出MN的长,则可表示出△BCN的面积,由条件可求得D点坐标.
解答 解:
(1)∵∠ACB=90°,
∴∠ACO+∠OCB=∠OBC+∠OCB=90°,
∴∠ACO=∠OBC,且∠AOC=∠COB,
∴△AOC∽△COB,
∴$\frac{AO}{CO}$=$\frac{CO}{BO}$,
∵A(-1,0),B(4,0),
∴OA=1,OB=4,
∴OC2=OA•OB=4,即OC=2,
∴C(0,2),
把A、B、C三点坐标代入抛物线解析式可得$\left\{\begin{array}{l}{a-b+c=0}\\{16a+4b+c=0}\\{c=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\\{c=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(2)当AB为对角线时,
∵A、B关于对称轴对称,D在抛物线,H在对称轴上,
∴AB为四边形AHBD的对角线,
∴D点为抛物线的顶点坐标,
∵y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{25}{8}$,
∴D点坐标为($\frac{3}{2}$,$\frac{25}{8}$);
当AB为边时,则有AB∥DH,且AB=DH,
设D(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2),则DH=|x-$\frac{3}{2}$|,
∵A(-1,0),B(4,0),
∴AB=5,
∴|x-$\frac{3}{2}$|=5,解得x=$\frac{13}{2}$或x=-$\frac{7}{2}$,
此时点D的坐标为($\frac{13}{2}$,-$\frac{75}{8}$)或(-$\frac{7}{2}$,-$\frac{75}{2}$);
综上可知D点坐标为($\frac{3}{2}$,$\frac{25}{8}$)或($\frac{13}{2}$,-$\frac{75}{8}$)或(-$\frac{7}{2}$,-$\frac{75}{2}$);
(3)如图,过N作NM∥y轴,交BC于点M,
∵B(4,0),C(0,2),
∴可设直线BC解析式为y=kx+2,
把B点坐标代入可得0=4k+2,解得k=-$\frac{1}{2}$,
∴直线BC解析式为y=-$\frac{1}{2}$x+2,
设N(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2),则M(x,-$\frac{1}{2}$x+2),
∴MN=|-$\frac{1}{2}$x2+$\frac{3}{2}$x+2-(-$\frac{1}{2}$x+2)|=|-$\frac{1}{2}$x2+2x|,
∴S△BCN=$\frac{1}{2}$MN•OB=$\frac{1}{2}$×4|-$\frac{1}{2}$x2+2x|=2|-$\frac{1}{2}$x2+2x|=|-x2+4x|,
当S△BCN=4时,则有|-x2+4x|=4,解得x=2或x=2+$\sqrt{2}$或x=2-$\sqrt{2}$,
∴存在满足条件的点N,这样的点有三个.
点评 本题为二次函数的综合应用,涉及待定系数法、平行四边形的判定和性质、相似三角形的判定和性质、三角形的面积及方程思想等知识.在(1)中求得C点坐标是解题的关键,在(2)中确定出D点的位置是解题的关键,在(3)用N点坐标表示出△BCN的面积是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | 2019 | B. | 2018 | C. | 2016 | D. | 2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,反比例函数y=$\frac{3}{2x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动,tan∠CAB=2,则关于x的方程x2-5x+k=0的解为x1=-1,x2=6.
如图,反比例函数y=$\frac{3}{2x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动,tan∠CAB=2,则关于x的方程x2-5x+k=0的解为x1=-1,x2=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
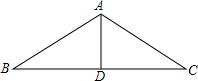 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°).
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前单价x (元) | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后单价y (元) | y1 | y2=4 | y3=59 | y4 | … | yn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com