
 [问题提出]
[问题提出]分析 (1)借助“HL”直接得出结论;
(2)先构造出△A'C'B∽△ACB,进而判断出Rt△A'C'B≌Rt△DFE即可得出结论;
(3)先构造出△AGC∽△DHF,借助(2)的结论即可得出结论.
解答 解:(1)斜边和一条直角边对应成比例的两直角三角形相似,
故答案为:斜边和一条直角边对应成比例的两直角三角形相似;
(2)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,若 $\frac{DE}{AB}=\frac{DF}{AC}$,则△ABC∽△DEF.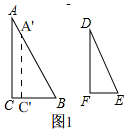
理由:在BA上取一点A'使BA'=DE,过点A'作AC'∥AC交BC于C',
∴∠A'C'B=∠C=90°=∠F,△A'C'B∽△ACB,
∴$\frac{A'B}{AB}=\frac{A'C'}{AC}$,
∵$\frac{DE}{AB}=\frac{DF}{AC}$,
∴$\frac{A'B}{A'C'}=\frac{DE}{DF}$,
∵BA'=DE,
∴A'C'=DF
在Rt△A'C'B和Rt△DFE中,$\left\{\begin{array}{l}{DE=A'B}\\{DF=A'C'}\end{array}\right.$,
∴Rt△A'C'B≌Rt△DFE(HL),
∵△A'C'B∽△ACB,
∴△DFE∽△ACB;
故答案为若 $\frac{DE}{AB}=\frac{DF}{AC}$;
(3)成立,如图2,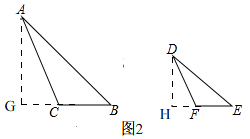
过点A作AG⊥BC交BC的延长线于G,过点D作DH⊥EF交EF的延长线于H,
∴∠G=∠H=90°,
∵∠ACB=∠DFE,
∴∠ACG=∠DFH,
∴△AGC∽△DHF,
∴$\frac{AC}{DF}=\frac{AG}{DH}$,
∵$\frac{AB}{DE}=\frac{AC}{DF}$,
∴$\frac{AB}{DE}=\frac{AG}{DH}$,
用(2)的结论得,△ABC∽△DEF.
点评 此题是相似形综合题,主要考查了类比的思想,相似三角形的判定和性质,全等三角形的判定和性质,解本题的关键是构造相似三角形,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
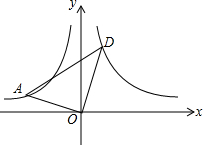 如图,∠AOB=90°,且点A,B分别在反比例函数y=$\frac{{k}_{1}}{x}$(x<0),y=$\frac{{k}_{2}}{x}$(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
如图,∠AOB=90°,且点A,B分别在反比例函数y=$\frac{{k}_{1}}{x}$(x<0),y=$\frac{{k}_{2}}{x}$(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
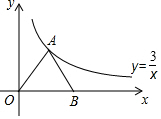 已知反比例函数y=$\frac{3}{x}$在第一象限的图象如图所示,点A是在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=3.
已知反比例函数y=$\frac{3}{x}$在第一象限的图象如图所示,点A是在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
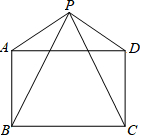 如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.
如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上的一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是1.
如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上的一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com