
| 6 |
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
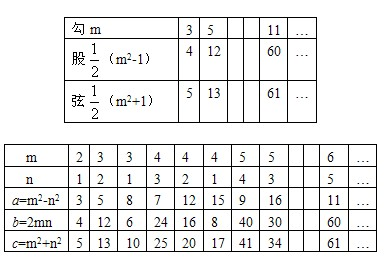
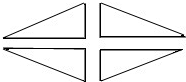
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 房价y(元) | 550 | 500 | 450 | 400 | 350 | 300 | 300 | 300 | 300 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (m2-1)和c=
(m2-1)和c= (m2+1)是勾股数.
(m2+1)是勾股数.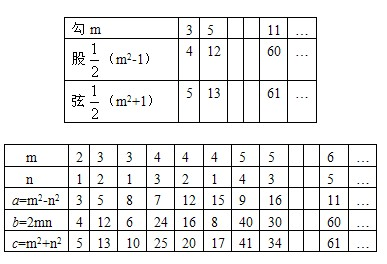
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校九年级一班数学科代表对本班期末考试数学成绩(成绩去整数,满分为100分)作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
| 分组 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
(1)在频数、频率统计表中a=______;b=______;并将频数分布直方图补充完整.
(2)若该校九年级共有12个班,每班人数相同,成绩在79.5以上的为A级,请你估算在此次考试中,全年级学生数学成绩为A级的人数为多少人?
(3)若在本班49.5~59.5和89.5~100.5两个分数段任选两名同学,求这两名同学成绩之差的绝对值不大于10分的概率是多少?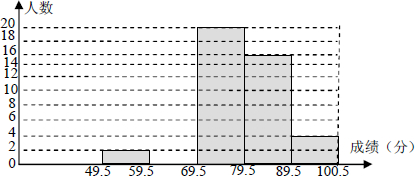
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com