
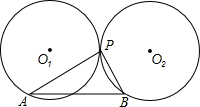
 已知:如图,两个半径长为r的等圆⊙O1和⊙O2外切于点P,A是⊙O1上的一点,BP⊥AP,BP交⊙O2于点B.求证:AB=2r.
已知:如图,两个半径长为r的等圆⊙O1和⊙O2外切于点P,A是⊙O1上的一点,BP⊥AP,BP交⊙O2于点B.求证:AB=2r. 分析 连接O1O2,AO1,BO2,只要证明四边形ABO2O1是平行四边形即可解决问题.
解答 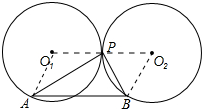 证明:连接O1O2,AO1,BO2
证明:连接O1O2,AO1,BO2
∵⊙O1和⊙O2外切于点P,
∴接O1O2经过点P,
∵PA⊥PB,
∴∠APB=90°,
∴∠PAB+∠PBA=90°,∠APO1+∠BPO2=90°,
∵O1A=O1P,O2P=O2B,
∴∠O1AP=∠O1PA,∠O2PB=∠O2BP,
∴∠O1AB+∠O2BA=∠O1AP+∠PAB+∠PBA+∠O2BP=180°,
∴AO1∥BO2,
∵AO1=BO2,
∴四边形ABO2O1是平行四边形,
∴AB=O1O2=2r.
点评 本题考查相切两个圆的性质,平行四边形的判定和性质等知识,解题的关键是添加辅助线,构造特殊四边形,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
 如图,BD是⊙O的直径,点A、C在⊙O上,$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则∠BDC的度数是( )
如图,BD是⊙O的直径,点A、C在⊙O上,$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则∠BDC的度数是( )| A. | 60° | B. | 45° | C. | 35° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
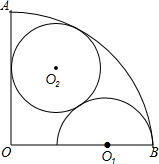 如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )
如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )| A. | 32cm | B. | 31cm | C. | 9cm | D. | 18cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数a、b、c的大小关系如图所示,则下列式子中一定成立的是( )
有理数a、b、c的大小关系如图所示,则下列式子中一定成立的是( )| A. | a+b+c>0 | B. | |a+b|<c | C. | |a-c|=|a|+c | D. | |b-c|>|c-a| |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条对角线互相垂直平分的四边形是菱形 | |
| B. | 两条对角线相等且互相垂直的四边形是矩形 | |
| C. | 有两个角相等的梯形是等腰梯形 | |
| D. | 两条对角线平分且相等的四边形是正方形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com