
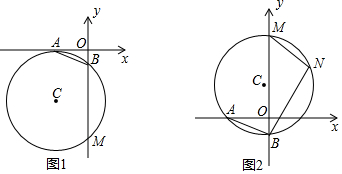
分析 (1)设⊙C的半径为r,连接CA,CB,过C作CD⊥y轴于D,由BD2+CD2=BC2,可得(r-1)2+32=r2,进而得到BD=4,根据tan∠CBM=$\frac{CD}{BD}$进行计算即可;
(2)①当点C在y轴上时,设半径CA=CB=r,则CO=r-1,由CO2+AO2=AC2,可得(r-1)2+32=r2,进而得到BM=2r=10,过N作NE⊥BM于E,连接NC,根据△BMN的面积=$\frac{1}{2}$BM×NE≤$\frac{1}{2}$BM×NC,即可得出当E与C重合时,BMN的面积最大;
②根据当圆心C移动到G(-3,-5)时,圆与x轴相切,连接GA,GB,延长GA交⊙C于F,过G作GH⊥y轴于H,根据tan∠HBG=$\frac{3}{4}$=tan∠MBN,可得点N在直线GB上,根据CR=CS,可知AF=BN,进而得到|BM-BN|=|BM-AF|=2BO=2.
解答 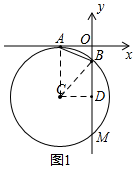 解:(1)设⊙C的半径为r,
解:(1)设⊙C的半径为r,
如图1,连接CA,CB,过C作CD⊥y轴于D,则四边形ACDO是矩形,BD=$\frac{1}{2}$BM,
∴CD=AO=3,DO=CA=r,BD=r-1,CB=CA=r,
由BD2+CD2=BC2,可得(r-1)2+32=r2,
解得r=5,
∴BD=4,
∴tan∠CBM=$\frac{CD}{BD}$=$\frac{3}{4}$;
(2)①如图2,当点C在y轴上时,设半径CA=CB=r,则CO=r-1,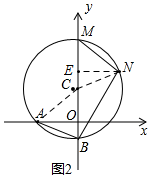
由CO2+AO2=AC2,可得(r-1)2+32=r2,
解得r=5,
∴BM=2r=10,
过N作NE⊥BM于E,连接NC,则NE≤NC,
∴△BMN的面积=$\frac{1}{2}$BM×NE≤$\frac{1}{2}$BM×NC,
∴当E与C重合时,NE=NC,△BMN的面积最大,
此时,△BMN的面积=$\frac{1}{2}$BM×NC=25,
②当tan∠MBN=$\frac{3}{4}$时,|BM-BN|的值不随⊙C大小的变化而变化,理由如下: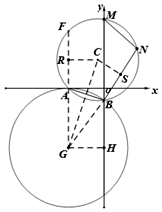
由(1)知,当圆心C移动到G(-3,-5)时,圆与x轴相切,如图3,
连接GA,GB,延长GA交⊙C于F,过G作GH⊥y轴于H,
∴AF∥BM,
由CG垂直平分AB,可得GC平分∠FGB,
∵GH=3,HB=4,
∴tan∠HBG=$\frac{3}{4}$=tan∠MBN,
∴∠HBG=∠MBN,
∴点N在直线GB上,
过C作CR⊥GF于R,CS⊥GN于S,则CR=CS,
∴AF=BN,
∴|BM-BN|=|BM-AF|=2BO=2,
故当tan∠MBN=$\frac{3}{4}$时,|BM-BN|的值不随⊙C大小的变化而变化,|BM-BN|=2.
点评 本题属于圆的综合题,主要考查了垂径定理,矩形的判定与性质,勾股定理的运用,三角形的面积的计算以及锐角三角函数的综合应用,解决问题的关键是作辅助线构造直角三角形,依据勾股定理列方程求解.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.075 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
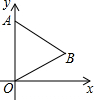 如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2017次后,顶点B的坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).
如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2017次后,顶点B的坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com