
【题目】点(2,﹣4)在反比例函数y= ![]() 的图象上,则下列各点在此函数图象上的是( )
的图象上,则下列各点在此函数图象上的是( )
A.(2,4)
B.(﹣1,﹣8)
C.(﹣2,﹣4)
D.(4,﹣2)
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
点A、B在数轴上分别表示两个数a、b,A、B两点间的距离记为|AB|,O表示原点.当A、B两点中有一点在原点时,不妨设点A为原点,如图1,则|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时,
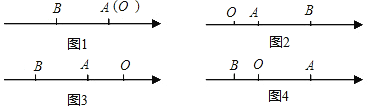
①如图2,若点A、B都在原点的右边时,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如图3,若点A、B都在原点的左边时,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
③如图4,若点A、B在原点的两边时,|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|.
回答下列问题:
(1)综上所述,数轴上A、B两点间的距离为|AB|=______.
(2)若数轴上的点A表示的数为3,点B表示的数为-4,则A、B两点间的距离为______;
(3)若数轴上的点A表示的数为x,点B表示的数为-2,则|AB|=______,若|AB|=3,则x的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.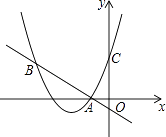
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】油电混动汽车是一种节油、环保的新技术汽车.它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中.汽车在低速行驶时,使用蓄电池带动电动机驱动汽车,节约燃油.某品牌油电混动汽车与普通汽车的相关成本数据估算如下:
油电混动汽车 | 普通汽车 | |
购买价格 | 17.48 | 15.98 |
每百公里燃油成本(元) | 31 | 46 |
某人计划购入一辆上述品牌的汽车.他估算了未来10年的用车成本,在只考虑车价和燃油成本的情况下,发现选择油电混动汽车的成本不高于选择普通汽车的成本.则他在估算时,预计平均每年行驶的公里数至少为( )
A. 5000 B. 10000 C. 15000 D. 20000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,D是 ![]() 上一点,OD⊥BC,垂足为H.
上一点,OD⊥BC,垂足为H. 
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;
(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=5 ![]() ,BN=3
,BN=3 ![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com