
| A. | $(3,\frac{9}{2})$ | B. | $(\frac{4}{3},6)$ | C. | $(3,\frac{9}{2})或(-3,-\frac{9}{2})$ | D. | $(\frac{4}{3},6)或(-\frac{4}{3},-6)$ |
分析 由于△ABC与△A′B′C′的相似比为$\frac{2}{3}$,则是把△ABC放大$\frac{3}{2}$倍,根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,于是把A(2,3)都乘以$\frac{3}{2}$或-$\frac{3}{2}$即可得到A′的坐标.
解答 解:∵△ABC与△A′B′C′的相似比为$\frac{2}{3}$,
∴△A′B′C′与△ABC的相似比为$\frac{3}{2}$,
∵位似中心为原点0,
∴A′(2×$\frac{3}{2}$,3×$\frac{3}{2}$)或A′(-2×$\frac{3}{2}$,-3×$\frac{3}{2}$),
即A′(3,$\frac{9}{2}$)或A′(-3,-$\frac{9}{2}$).
故选C.
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.
我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
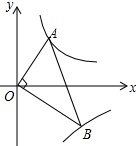 如图,第一角限内的点A在反比例函数$y=\frac{2}{x}$的图象上,第四象限内的点B 在反比例函数$y=\frac{k}{x}$图象上,且OA⊥OB,∠OAB=60度,则k值为-6.
如图,第一角限内的点A在反比例函数$y=\frac{2}{x}$的图象上,第四象限内的点B 在反比例函数$y=\frac{k}{x}$图象上,且OA⊥OB,∠OAB=60度,则k值为-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com