
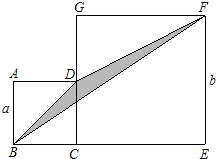
 四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )
四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )| A. | ab | B. | $\frac{1}{2}$ab | C. | $\frac{1}{2}$b2 | D. | $\frac{1}{2}$a2 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
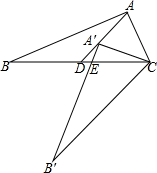 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.
如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
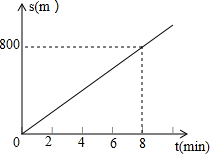 小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题:
小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
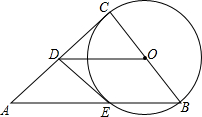 在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE.
在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com