
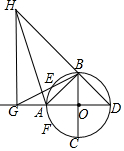
 设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角.
设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角. 分析 连接AC、AE、CF、DE,由AD、BC是圆O的互相垂直的直径,得出AB=AC,AB⊥DE,∠CAD=∠BAD=∠BED=45°,$\widehat{AE}=\widehat{AF}$,$\widehat{AB}=\widehat{AC}$,得出$\widehat{BE}=\widehat{CF}$,由圆周角定理得出∠BAE=∠CAF=∠BDE,由角的关系得出∠HAG=∠HBG,证出H、G、A、B四点共圆,即可得出结论.
解答 证明:连接AC、AE、CF、DE,如图所示: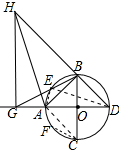
∵AD、BC是圆O的互相垂直的直径,
∴AB=AC,AB⊥DE,∠CAD=∠BAD=∠BED=45°,
∵$\widehat{AE}=\widehat{AF}$,$\widehat{AB}=\widehat{AC}$,$\widehat{BE}=\widehat{CF}$,
∴∠BAE=∠CAF=∠BDE,
∵∠HAG=∠DAF=∠CAD+∠CAF=45°+∠CAF,∠HBG=∠BED+∠BDE=45°+∠BDE,
∴∠HAG=∠HBG,
∴H、G、A、B四点共圆,
∴∠HGA=∠HBA=90°.
点评 本题考查了圆周角定理、四点共圆等知识;熟练掌握圆周角定理,证明四点共圆是解决问题的关键.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
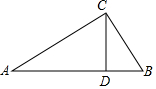 如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:
如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
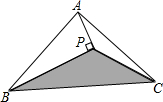 如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )| A. | 10cm2 | B. | 12cm2 | C. | 16cm2 | D. | 20cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
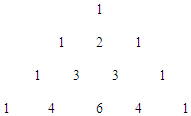 我们已经知道:
我们已经知道:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com