
����Ŀ������ij�̳��мס���������Ʒ������ÿ������15Ԫ���ۼ�20Ԫ������ÿ������35Ԫ���ۼ�45Ԫ��
��1�����̼�ͬʱ�����ס���������Ʒ100���������Ʒ����x���������������Ʒ������Ϊy Ԫ��д��y��x�ĺ�����ϵʽ��
��2�����̼Ҽƻ����Ͷ��3000Ԫ���ڹ�����������Ʒ��100����������Ҫ�������ټ�������Ʒ����������Щ��Ʒ���̼ҿɻ�õ���������Ƕ���Ԫ��
��3������һ���ڼ䣬�̼ҶԼס���������Ʒ���б��е��Żݻ��С�������̳�һ���Ը���324Ԫ���������Ʒ���̼ҿɻ�õ���С��������������Ƕ��٣�
����ǰһ���Թ����ܽ�� | �Żݴ�ʩ |
������400Ԫ | �ۼ۴���� |
����400Ԫ | �ۼ۴���� |
���𰸡�
��1���⣺�����Ʒ����x����������Ʒ������100��x�����������⣬��
y=��20��15��x+��45��35����100��x��=��5x+1000��
��y��x֮��ĺ�����ϵʽΪ��y=��5x+1000��
��2���⣺�����⣬��15x+35��100��x����3000��
��֮����x��25��
��y=��5x+1000��k=��5��0��
��y��x�����������
�൱xȡ��Сֵ25ʱ��y���ֵ����ʱy=��5��25+1000=875��Ԫ����
������Ҫ����25��������Ʒ����������Щ��Ʒ���̼ҿɻ�õ����������875Ԫ��
��3���⣺��С�������̳����������Ʒm��������������Ʒn����
�� ������ǰһ���Թ����ܽ�����400ʱ�������ܽ��Ϊ324��0.9=360��Ԫ����
��20m+45n=360��m=18�� ![]() n��0����0��n��8��
n��0����0��n��8��
n��4�ı�������3�������
���1��m=0��n=8���������ǣ�324��8��35=44��Ԫ����
���2��m=9��n=4���������ǣ�324����15��9+35��4��=49��Ԫ����
���3��m=18��n=0���������ǣ�324��15��18=54��Ԫ����
�� ������ǰһ���Թ����ܽ���400ʱ�������ܽ��Ϊ324��0.8=405��Ԫ����
�� ��20m+45n=405��m= ![]() ��0����0��n��9��
��0����0��n��9��
m��n��������������3�������
���1��m=9��n=5��������Ϊ��324����9��15+5��35��=14��Ԫ����
���2��m=18��n=1��������Ϊ��324����18��15+1��35��=19��Ԫ����
�����������̼ҿɻ�õ���С������14Ԫ�����������54Ԫ��
����������1����������=������Ʒ������+������Ʒ������Ϳ��Եó����ۣ���2�����ݡ��̼Ҽƻ����Ͷ��3000Ԫ���ڹ�����������Ʒ��100�����г�����ʽ���ⲻ��ʽ�����⣬�ٸ���һ�κ��������ʣ�����̼ҿɻ�õ��������3����С�������̳����������Ʒm��������������Ʒn����������������ۣ��ٴ���ǰһ���Թ����ܽ�����400���ڴ���ǰһ���Թ����ܽ���400��


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�BEƽ�֡�ABC��AC���ڵ�E��
(1)��ͼ1������E��DE��BC��AB�ڵ�D����֤����BDEΪ���������Σ�
(2)��ͼ2���ӳ�BE��D����ADB =��ABC�� AF��BD��F��AD=2,BF=3,��DF�ij�
(3)��ͼ3����AB=AC��AF��BD����ACD=![]() ��ABC���ж�BF��CD��DF��������ϵ����˵�����ɣ�
��ABC���ж�BF��CD��DF��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������֪�ı���ABCD����������ȣ��ĸ��ڽǶ�����90�㣬��E��CD����һ�㣬F��BC����һ�㣬����EAF=45�㣮
��1����֤��BF+DE=EF��
��2����AB=6����BF=x��DE=y����y����x�ĺ�������ʽ����д��x��ȡֵ��Χ��
��3������A��AH��FE�ڵ�H����ͼ��2������FH=2��EH=1ʱ������AFE�������
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=ax+b��a��0������κ���ax2+2x+b��a��0����ͬһֱ������ϵ�е�ͼ������ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ϊ�༶�����������һ��������Ϸ����Ϸ�������£���һ��������ֽ����װ�к졢�ơ���������ɫ��С�����dz���ɫ����ȫ��ͬ�����к�����2����������1����������1������Ϸ���ȴ�ֽ�����������һ����¼��ɫ��Żأ���С��ҡ�ȣ����������һ��������������������ɫ��ͬ������Ϸ�߿ɻ��һ�ݼ���Ʒ������������״ͼ���б�������Ϸ��ü���Ʒ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AE��һ���㣬�������A��E�غϣ�����AEͬ��ֱ�������ABC������CDE��AD��BE���ڵ�O��AD��BC�����P��BE��CD���ڵ�Q������PQ��
��֤����1��AD=BE
��2����APC�ա�BQC
��3����PCQ�ǵȱ������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����п�չ�ˡ�Ѱ�����㼣���Ļ��ij��ѧΪ���˽����꼶800��ѧ���ڡ�ѧ���¡��������µ������������������꼶50��ѧ����һ�����������µĴ����������������ݻ��Ƴ�ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺ ������������꼶50��ѧ����������������´�����ƽ������ �� ������ �� ������ ��
�ڸ����������ݣ����Ƹ�У���꼶800��ѧ���ڡ�ѧ���¡��������²�����4�ε�������
���𰸡��⣺��ƽ��������2��5+3��6+4��13+5��16+6��10����50=4.4��
������5��
���6��2=4��
�������²�����4�ε�������800�� ![]() =624��
=624��
��1���ڴ���2����ͬ��С�����Ƿֱ�д������1��2���ҿڴ���װ��3����ͬ��С�����Ƿֱ�д������3��4��5�����������ڴ��и������ȡ��1��С�� ���á���״ͼ�������б�������ʾ���п��ܳ��ֵĽ����
��ȡ��������С������д����֮����ż���ĸ����Ƕ��٣�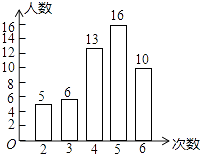
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϣ�������ıϴ����˹ѧ�ɰ�1��3��6��10������������Ϊ������������������1��4��9��16������������Ϊ����������������ͼ�п��Է��֣��κ�һ������1�������������������Կ�����������������������֮�ͣ����е�ʽ�У�������һ���ɵ��ǣ�������

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com