
°æƒø°ø»ÁÕº(1)£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„A°¢C∑÷±‘⁄y÷·∫Õx÷·…œ£¨AB°Œx÷·£¨cosB£Ω![]() £Æµ„P¥”Bµ„≥ˆ∑¢£¨“‘1cm/sµƒÀŸ∂»—ÿ±þBA‘»ÀŸ‘À∂Ø£¨µ„Q¥”µ„A≥ˆ∑¢£¨—ÿœþ∂ŒAO£≠OC£≠CB‘»ÀŸ‘À∂أƵ„P”ε„QÕ¨ ±≥ˆ∑¢£¨∆‰÷–“ªµ„µΩ¥Ô÷’µ„£¨¡Ì“ªµ„“≤ÀÊ÷ÆÕ£÷π‘À∂أƅ˵„P‘À∂صƒ ±º‰Œ™t(s)£¨°˜BPQµƒ√ʪ˝Œ™S(cm2)£¨ “—÷™S”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕº(2)÷–µƒ«˙œþ∂ŒOE°¢œþ∂ŒEF”Ϋ˙œþ∂ŒFG£Æ
£Æµ„P¥”Bµ„≥ˆ∑¢£¨“‘1cm/sµƒÀŸ∂»—ÿ±þBA‘»ÀŸ‘À∂Ø£¨µ„Q¥”µ„A≥ˆ∑¢£¨—ÿœþ∂ŒAO£≠OC£≠CB‘»ÀŸ‘À∂أƵ„P”ε„QÕ¨ ±≥ˆ∑¢£¨∆‰÷–“ªµ„µΩ¥Ô÷’µ„£¨¡Ì“ªµ„“≤ÀÊ÷ÆÕ£÷π‘À∂أƅ˵„P‘À∂صƒ ±º‰Œ™t(s)£¨°˜BPQµƒ√ʪ˝Œ™S(cm2)£¨ “—÷™S”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕº(2)÷–µƒ«˙œþ∂ŒOE°¢œþ∂ŒEF”Ϋ˙œþ∂ŒFG£Æ
£®1£©µ„Qµƒ‘À∂ØÀŸ∂»Œ™ cm/s£¨µ„Bµƒ◊¯±ÍŒ™ £ª
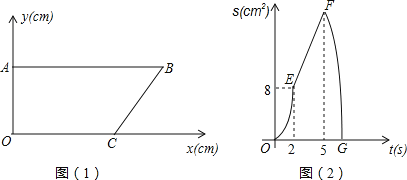
£®2£©«Û«˙œþFG∂Œµƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®3£©µ±tŒ™∫Œ÷µ ±£¨°˜BPQµƒ√ʪ˝ «Àƒ±þ–ŒOABCµƒ√ʪ˝µƒ![]() £ø
£ø
°æ¥∞∏°ø£®1£©4,(18,8)£ª
£®2£©«˙œþFG∂Œµƒ∫Ø ˝Ω‚Œˆ ΩŒ™£∫S=![]() t2+12t£ª
t2+12t£ª
£®3£©t=3ªÚt=![]() ,°˜BPQµƒ√ʪ˝ «Àƒ±þ–ŒOABCµƒ√ʪ˝µƒ
,°˜BPQµƒ√ʪ˝ «Àƒ±þ–ŒOABCµƒ√ʪ˝µƒ![]() .
.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©Ω·∫œ∫Ø ˝ÕºœÛµ√≥ˆµ±2√Î ±£¨BP=2£¨¥À ±°˜BPQµƒ√ʪ˝Œ™8cm2£¨Ω¯∂¯«Û≥ˆAOŒ™8cm£¨º¥ø…µ√≥ˆQµ„µƒÀŸ∂»£¨Ω¯∂¯«Û≥ˆABµƒ≥§º¥ø…£ª£®2£© ◊œ»µ√≥ˆPB=t£¨BQ=30-4t£¨‘ÚQM=![]() £®30-4t£©=24-
£®30-4t£©=24-![]() t£¨¿˚”√S°˜PBQ=
t£¨¿˚”√S°˜PBQ=![]() t£®24-
t£®24-![]() t£©«Û≥ˆº¥ø…£ª£®3£© ◊œ»µ√≥ˆ°˜BPQµƒ√ʪ˝£¨Ω¯∂¯µ√≥ˆFµ„◊¯±Í£¨Ω¯∂¯µ√≥ˆ÷±œþEFΩ‚Œˆ ΩŒ™£∫S=4t£¨µ±S=12 ±£¨«Û≥ˆtµƒ÷µ£¨‘ŸΩ´S=12¥˙»ÎS=-
t£©«Û≥ˆº¥ø…£ª£®3£© ◊œ»µ√≥ˆ°˜BPQµƒ√ʪ˝£¨Ω¯∂¯µ√≥ˆFµ„◊¯±Í£¨Ω¯∂¯µ√≥ˆ÷±œþEFΩ‚Œˆ ΩŒ™£∫S=4t£¨µ±S=12 ±£¨«Û≥ˆtµƒ÷µ£¨‘ŸΩ´S=12¥˙»ÎS=-![]() t2+12t«Û≥ˆtµƒ÷µ£¨º¥ø…µ√≥ˆ¥∞∏£Æ
t2+12t«Û≥ˆtµƒ÷µ£¨º¥ø…µ√≥ˆ¥∞∏£Æ
‘Ã‚Ω‚Œˆ£∫(1)”…“‚ø…µ√≥ˆ£∫µ±2√Î ±£¨°˜BPQµƒ√ʪ˝µƒ∫Ø ˝πÿœµ Ω∏ƒ±‰£¨‘ÚQ‘⁄AO…œ‘À∂Ø2√Σ¨
µ±2√Î ±£¨BP=2£¨¥À ±°˜BPQµƒ√ʪ˝Œ™8cm2£¨
°ýAOŒ™8cm£¨
°ýµ„Qµƒ‘À∂ØÀŸ∂»Œ™£∫8°¬2=4(cm/s)£¨
µ±‘À∂صΩ5√Î ±£¨∫Ø ˝πÿœµ Ω∏ƒ±‰£¨‘ÚCO=12cm£¨
°þcosB=![]() £¨
£¨
°ýø…«Û≥ˆAB=6+12=18(cm)£¨
°ýB(18,8)£ª
π ¥∞∏Œ™£∫4£¨(18£¨8)£ª
(2)»ÁÕº(1)£∫

PB=t£¨BQ=304t£¨
π˝µ„Q◊˜QM°ÕAB”⁄µ„M£¨
‘ÚQM=![]() (304t)=24
(304t)=24![]() t£¨
t£¨
°ýS°˜PBQ=![]() t(24
t(24![]() t)=
t)= ![]() t2+12t(5t7.5)£¨
t2+12t(5t7.5)£¨
º¥«˙œþFG∂Œµƒ∫Ø ˝Ω‚Œˆ ΩŒ™£∫S= ![]() t2+12t£ª
t2+12t£ª
(3)°þSÃð–ŒOABC=![]() (12+18)°¡8=120£¨
(12+18)°¡8=120£¨
°ý![]() °¡120=12£¨
°¡120=12£¨
µ±t>2 ±£¨F(5£¨20)£¨
°ý÷±œþEFΩ‚Œˆ ΩŒ™£∫S=4t£¨µ±S=12 ±£¨4t=12£¨Ω‚µ√£∫t=3£¨
Ω´S=12¥˙»ÎS=![]() t2+12t£¨
t2+12t£¨
Ω‚µ√£∫t=![]() £¨
£¨
°þ5t7.5£¨π t=![]() £¨
£¨
◊€…œÀ˘ ˆ£∫t=3ªÚt=![]() £¨°˜BPQµƒ√ʪ˝ «Àƒ±þ–ŒOABCµƒ√ʪ˝µƒ
£¨°˜BPQµƒ√ʪ˝ «Àƒ±þ–ŒOABCµƒ√ʪ˝µƒ![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄µ»—¸°˜ABCµƒ¡Ω—¸AB°¢BC…œ∑÷±»°µ„D∫ÕE£¨ πDB=DE£¨¥À ±«°”–°œADE= ![]() °œACB£¨‘Ú°œBµƒ∂» ˝ « £Æ
°œACB£¨‘Ú°œBµƒ∂» ˝ « £Æ 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“√«÷™µ¿∂‘”⁄x÷·…œµƒ»Œ“‚¡Ωµ„A£®x1£¨0£©£¨B£®x2£¨0£©£¨”–AB=|x1©Åx2|£¨∂¯∂‘”⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–µƒ»Œ“‚¡Ωµ„P1£®x1£¨y1£©£¨P2£®x2£¨y2£©£¨Œ“√«∞—|x1©Åx2|+|y1©Åy2|≥∆Œ™Pl£¨P2¡Ωµ„º‰µƒ÷±Ω«æý¿Î£¨º«◊˜d£®P1£¨P2£©£¨º¥d£®P1£¨P2£©=|x1©Åx2|+|y1©Åy2|£Æ
£®1£©“—÷™OŒ™◊¯±Í‘≠µ„£¨»Ùµ„P◊¯±ÍŒ™£®1£¨3£©£¨‘Úd£®O£¨P£©=°° °°£ª
£®2£©“—÷™OŒ™◊¯±Í‘≠µ„£¨∂ص„P£®x£¨y£©¬˙◊„d£®O£¨P£©=2£¨«Î–¥≥ˆx”Îy÷ƺ‰¬˙◊„µƒπÿœµ Ω£¨≤¢‘⁄À˘∏¯µƒ÷±Ω«◊¯±Íœµ÷–ª≠≥ˆÀ˘”–∑˚∫œÃıº˛µƒµ„PÀ˘◊È≥…µƒÕº–Œ£ª
£®3£© ‘«Ûµ„M£®2£¨3£©µΩ÷±œþy=x+2µƒ◊Ó–°÷±Ω«æý¿Î£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
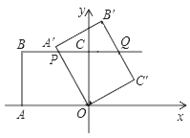
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨OŒ™◊¯±Í‘≠µ„£¨µ„Aµƒ◊¯±ÍŒ™£®£≠8£¨0£©£¨÷±œþBCæ≠π˝µ„B£®£≠8£¨6£©£¨C£®0£¨6£©£¨Ω´Àƒ±þ–ŒOABC»∆µ„O∞¥À≥ ±’Î∑ΩœÚ–˝◊™¶¡∂»£®0£º¶¡ °Ð180°„£©µ√µΩÀƒ±þ–ŒOA°‰B°‰C°‰£¨¥À ±÷±œþOA°‰°¢÷±œþB°‰C°‰∑÷±”Î÷±œþBCœýΩª”⁄P°¢Q£Æ‘⁄Àƒ±þ–ŒOABC–˝◊™π˝≥Ã÷–£¨»ÙBP£Ω![]() BQ£¨‘Úµ„Pµƒ◊¯±ÍŒ™__________£Æ
BQ£¨‘Úµ„Pµƒ◊¯±ÍŒ™__________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–º∆À„’˝»∑µƒ «£® £©
A. x2©Å2xy2£Ω©Åx2yB. 2a©Å3b£Ω©Åab
C. a2+a3£Ωa5D. ©Å3ab©Å3ab£Ω©Å6ab
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() ”Î
”Î![]() ÷·°¢
÷·°¢![]() ÷·∑÷±Ωª”⁄µ„
÷·∑÷±Ωª”⁄µ„![]() °¢
°¢![]() £¨µ„
£¨µ„![]() Œ™
Œ™![]() ÷·∏∫∞Î÷·…œ“ªµ„£¨
÷·∏∫∞Î÷·…œ“ªµ„£¨ ![]() ”⁄µ„
”⁄µ„![]() Ωª
Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £Æ“—÷™≈◊ŒÔœþ
£Æ“—÷™≈◊ŒÔœþ![]() æ≠π˝µ„
æ≠π˝µ„![]() °¢
°¢![]() °¢
°¢![]() £Æ
£Æ
£®![]() £©«Û≈◊ŒÔœþµƒ∫Ø ˝ Ω£Æ
£©«Û≈◊ŒÔœþµƒ∫Ø ˝ Ω£Æ
£®![]() £©¡¨Ω”
£©¡¨Ω”![]() £¨µ„
£¨µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ∑Ωµƒ≈◊ŒÔœþ…œ£¨¡¨Ω”
…œ∑Ωµƒ≈◊ŒÔœþ…œ£¨¡¨Ω”![]() °¢
°¢![]() £¨»Ù
£¨»Ù![]() ∫Õ
∫Õ![]() √ʪ˝¬˙◊„
√ʪ˝¬˙◊„![]() £¨«Ûµ„
£¨«Ûµ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
£®![]() £©»ÁÕº
£©»ÁÕº![]() £¨
£¨ ![]() Œ™
Œ™![]() ÷–µ„£¨…Ë
÷–µ„£¨…Ë![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œ“ªµ„£®≤ª∫¨∂Àµ„£©£¨¡¨Ω”
…œ“ªµ„£®≤ª∫¨∂Àµ„£©£¨¡¨Ω”![]() £Æ“ª∂ص„
£Æ“ª∂ص„![]() ¥”
¥”![]() ≥ˆ∑¢£¨—ÿœþ∂Œ
≥ˆ∑¢£¨—ÿœþ∂Œ![]() “‘√ø√Î
“‘√ø√Î![]() ∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩ
∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩ![]() £¨‘Ÿ—ÿ◊≈œþ∂Œ
£¨‘Ÿ—ÿ◊≈œþ∂Œ![]() “‘√ø√Î
“‘√ø√Î![]() ∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩ
∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩ![]() ∫ÛÕ£÷π£Æ»Ùµ„
∫ÛÕ£÷π£Æ»Ùµ„![]() ‘⁄’˚∏ˆ‘À∂Øπ˝≥Ã÷–”√ ±◊Ó…Ÿ£¨«Î÷±Ω”–¥≥ˆ◊Ó…Ÿ ±º‰∫Õ¥À ±µ„
‘⁄’˚∏ˆ‘À∂Øπ˝≥Ã÷–”√ ±◊Ó…Ÿ£¨«Î÷±Ω”–¥≥ˆ◊Ó…Ÿ ±º‰∫Õ¥À ±µ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥µÿ«¯Œ™¡Àπƒ¿¯ –√ÒΩ⁄‘º”√ÀÆ£¨º∆ªÆ µ––…˙ªÓ”√ÀÆ∞¥Ω◊Ãð ΩÀƺ€º∆∑—£¨√ø‘¬”√ÀÆ¡ø≤ª≥¨π˝10∂÷(∫¨10∂÷) ±£¨√ø∂÷∞¥ª˘¥°º€ ’∑—£ª√ø‘¬”√ÀÆ¡ø≥¨π˝10∂÷ ±£¨≥¨π˝µƒ≤ø∑÷√ø∂÷∞¥µ˜Ω⁄º€ ’∑—£Æ¿˝»Á£¨µ⁄“ª∏ˆ‘¬”√ÀÆ16∂÷£¨–ËΩªÀÆ∑—17.8‘™£¨µ⁄∂˛∏ˆ‘¬”√ÀÆ20∂÷£¨–ËΩªÀÆ∑—23‘™£Æ
£®1£©«Û√ø∂÷ÀƵƒª˘¥°º€∫Õµ˜Ω⁄º€£ª
£®2£©…Ë√ø‘¬”√ÀÆ¡øŒ™x∂÷£¨”¶ΩªÀÆ∑—Œ™y‘™£¨–¥≥ˆy”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
£®3£©»Ùƒ≥‘¬”√ÀÆ12∂÷£¨”¶ΩªÀÆ∑—∂ý…Ÿ‘™?
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™“ª∏ˆ»˝Ω«–Œµƒ¡Ω±þ≥§∑÷±Œ™3∫Õ4£¨‘Úµ⁄»˝±þµƒ≥§≤ªø…ƒÐµƒ «( )
A. 1 B. 2 C. 3 D. 4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com