
【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.若水面下降了2.5m,水面的宽度增加多少? 
【答案】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,把A点坐标(﹣2,0)代入得a=﹣0.5,
∴抛物线解析式为y=﹣0.5x2+2,
当水面下降2.5米,通过抛物线在图上的观察可转化为:
当y=﹣2.5时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,
可以通过把y=﹣2.5代入抛物线解析式得出: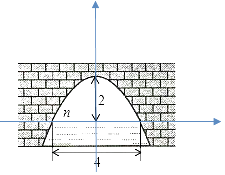
﹣2.5=﹣0.5x2+2,
解得:x=±3,
所以水面宽度增加到6米,比原先的宽度当然是增加了2米
【解析】根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=﹣2.5代入抛物线解析式得出水面宽度,即可得出答案.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】用同样规格的黑白两种颜色的正方形,按如图的方式拼图,请根据图中的信息完成下列的问题.

(1)在图②中用了 块黑色正方形,在图③中用了 块黑色正方形;
(2)按如图的规律继续铺下去,那么第![]() 个图形要用 块黑色正方形;
个图形要用 块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完90块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别从
,甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲速每小时
两地同时出发,甲速每小时![]() 千米,乙速每小时
千米,乙速每小时![]() 千米,请按下列要求列方程解题:
千米,请按下列要求列方程解题:
![]() 若同时出发,相向而行,多少小时相遇?
若同时出发,相向而行,多少小时相遇?
![]() 若同时出发,相向而行,多长时间后两车相距
若同时出发,相向而行,多长时间后两车相距![]() ?
?
![]() 若同时出发,同向而行,多长时间后两车相距
若同时出发,同向而行,多长时间后两车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.
(1)求证:四边形ACED是平行四边形;
(2)若AC=2,CE=4,求四边形ACEB的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2). 
(1)①将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
②平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(2)若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A. 4m厘米 B. 4n厘米 C. 2(m+n)厘米 D. 4(m-n)厘米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com