
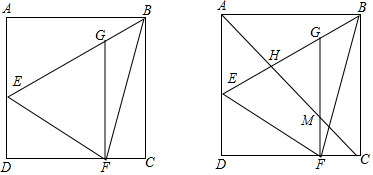
分析 (1)过点B作BN⊥EF于点N,由于FG∥AD可知∠AFG=∠FEG,从而可知EB是∠AEF的角平分线,由角平分线的性质可知AB=BN,由于AB=CB=BN,从而可知FB是∠EFC的角平分线,由角平分线的性质可知:∠NBF=∠CBF,从而可知∠EBN+∠NBF=45°.
(2)延长DA,使得AP=CF,连接PB,证明△APB≌△CFB(SAS),从而可知PB=FB,∠P=∠CFB,再证明△PEB≌△FEB(AAS),从而可知EP=EF,设MF=x,所以CF=x,EP=EF=4+x,由勾股定理可求出x=6,从而可知GM=4,再证明△AEH≌△MGH(AAS),从而可知MH=AH.
解答 解:(1)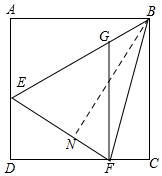 过点B作BN⊥EF于点N,
过点B作BN⊥EF于点N,
∵GF∥AD,
∴∠AEG=∠EGF,
∵EF=FG,
∴∠FEG=∠EGF,
∴∠AFG=∠FEG,
∴EB是∠AEF的角平分线,
由角平分线的性质可知:AB=BN,
∠ABE=∠NBE,
又∵AB=BC,
∴BN=BC,
∵BN⊥EF,BC⊥CF,
∴FB是∠EFC的角平分线,
由角平分线的性质可知:∠NBF=∠CBF,
∵∠ABE+∠EBN+∠NBF+∠CBF=90°,
∴∠EBN+∠NBF=45°,
即∠EBF=45°,
(2)延长DA,使得AP=CF,连接PB
在△APB与△CFB中,
$\left\{\begin{array}{l}{AP=CF}\\{∠PAB=∠FCB}\\{AB=BC}\end{array}\right.$
∴△APB≌△CFB(SAS)
∴PB=FB,∠P=∠CFB,
由(1)可知:∠EFB=∠CFB,
∴∠P=∠EFB
在△PEB与△FEB中,
$\left\{\begin{array}{l}{∠PEB=∠FEB}\\{∠P=∠EFB}\\{EB=EB}\end{array}\right.$,
∴△PEB≌△FEB(AAS),
∴EP=EF,
设MF=x,
∵∠ACD=45°,
∴CF=x,CM=$\sqrt{2}$x,
DF=12-x,
∵DE=2AE,
∴DE=8,AE=4,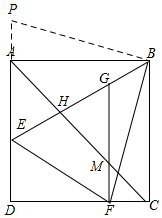
∵AP=CF=x,
∴EP=EF=4+x,
在Rt△DEF中,
∴由勾股定理可知:(4+x)2=(12-x)2+82,
解得:x=6,
∴CF=DF=6,
∵EF=PF=10,
∴GM=GF-MF=4,
∴AE=GM,
在△AEH与△MGH中,
$\left\{\begin{array}{l}{∠AEH=∠HGM}\\{∠AHE=∠MHG}\\{AE=GM}\end{array}\right.$,
∴△AEH≌△MGH(AAS),
∴AH=MH,
∵AM=AC-CM=12$\sqrt{2}$-6$\sqrt{2}$=6$\sqrt{2}$,
∴MH=$\frac{1}{2}$AM=3$\sqrt{2}$
点评 本题考查正方形的性质,涉及相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,解方程等知识,综合程度较高,需要学生灵活运用所知识.


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | (4) | B. | (3) | C. | (2) | D. | (1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,CB=CA,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知:如图,在△ABC中,CB=CA,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com