练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
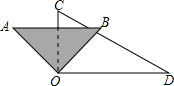
    3．如图，将一副三角板的直角顶点重合在一起，将三角板AOB绕点O的旋转过程中，下列结论成立的是（　　）
    A．∠AOD＞∠BOCB．∠AOC≠∠BODC．∠AOD-∠BOC=45°D．∠AOD+∠BOC=180°

    分析 依据旋转的性质可知∠AOB=∠COD=90°，然后依据图形间角的和差关系进行求解即可..

    解答 解：∵∠AOB=∠COD=90°，
    ∴∠AOD=∠AOB+∠COD-∠BOC．
    ∴∠AOD+∠BOC=∠AOB+∠COD=90°+90°=180°．
    故选：D．

    点评 本题主要考查的是旋转的性质、角的运算，明确在旋转过程中∠AOB和∠COD的度数不变是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．下列实数中，属于无理数的是（　　）
    A．-$\frac{1}{3}$B．0.1C．$\sqrt{4}$D．$\root{3}{9}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知抛物线y=x2-（5+a）x+5a与x轴交于定点A和另一点C，
    （1）求定点A的坐标；
    （2）点B（1，2）是抛物线y=x2-（5+a）x+5a与以坐标原点为圆心的圆的一个交点，试判断直线AB与圆位置关系；
    （3）在（2）中的抛物线上是否存在点P（P在点A的右上方），使△PAC、△PBC的面积相等？若存在，请求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

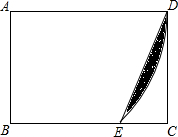    11．在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（　　）
    A．$\frac{π}{2}$-$\sqrt{2}$B．$\frac{π}{2}$-$\frac{\sqrt{2}}{2}$C．π-$\sqrt{2}$D．π-$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算：
    （1）（3.14-π）0+（-$\frac{1}{2}$）-2-2×2-1
    （2）（2a2+ab-2b2）（-$\frac{1}{2}$ab）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列命题：①两直线平行，同旁内角互补； ②三角形的外角和是180°； ③面积相等的三角形是全等三角形；④若n＜1，则n2-1＜0；其中，假命题的个数有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如果点M在y轴的左侧，且在x轴的上侧，到两坐标轴的距离都是1，则点M的坐标为（　　）
    A．（-1，2）B．（-1，-1）C．（-1，1）D．（1，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．若不等式组$\left\{\begin{array}{l}2x-4≤0\\ 1+x＞a\end{array}\right.$有解，则a的取值范围是（　　）
    A．a≤3B．a＜3C．a＜2D．a≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

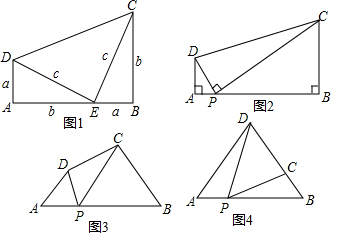    13．如图1是美国第20届总统加菲尔德于1876年公开发表的勾股定理一个简明证法，聪明的思齐和他的社团小朋友们发现：两个直角三角形在发生变化过程中，只要满足一定的条件，就会有神奇的结果：
    （1）问题：若把两个变换的三角形拼成如图2所示四边形ABCD，点P为AB上一点，且∠DPC=∠A=∠B=90°．
    求证：AD•BC=AP•BP．
    （2）探究：继续变换图形，如图3，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
    （3）应用：请利用（1）（2）获得的经验解决问题：如图4，在△ABD中，AB=12，AD=BD=10，点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，点C在边BD上，且满足∠DPC=∠A，问：经过几秒后CD长度等于D到AB的距离？

    查看答案和解析>>

    同步练习册答案