

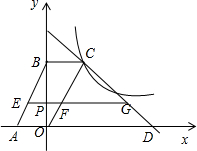
���� ��1���������A��B�����꣬����������COA����������C�����꣬����ֱ�߽���ʽ�����C�ĺ����꣬��C��-4��4������y=$\frac{k}{x}$������ȷ��k��ֵ��
��2���������P���꣬��ȷ����ֱ��AC��BG����ʽ������ȷ������D��E��F�����꣬���ɵó�DE��DF��ֱ�Ӽ��㼴�ɵó����ۣ�
��3����NE��MC��E����NF��OM��F����CG��x����G�����ı���CGON�������Σ�֤��C��M��O��N�ĵ㹲Բ������ͬ�����Ե�Բ�ܽ���ȣ����ɣ�
��� �⣺��1������ֱ��y=-$\frac{1}{2}$x+2����y=0ʱ��x=4����x=0ʱ��y=2��
��A��4��0����B��0��2����
��C��a��b����
��S��COA=$\frac{1}{2}$��4��b=8��
��b=4��
��C��a��4������y=-$\frac{1}{2}$x+2�ã�a=-4
��C��-4��4����
��C��-4��4������y=$\frac{k}{x}$�ã�
k=-16��
��2����P������m��n����
��A��G����y��Գƣ���A��4��0����
��G��-4��0����
��B��0��2����
��ֱ��BG����ʽΪy=$\frac{1}{2}$x+2��
�߹�P��PD��x����D���ֱ�BG��F��
��F��m��$\frac{1}{2}$m+2����D��m��0��
��DF=$\frac{1}{2}$m+2��
��A��4��0����C��-4��4����
��ֱ��AC����ʽΪy=-$\frac{1}{2}$x+2��
�߹�P��PD��x����D���ֱ�AC��E��
��E��m��-$\frac{1}{2}$m+2����
��DE=-$\frac{1}{2}$m+2��
��DE+DF=-$\frac{1}{2}$m+2+=$\frac{1}{2}$m+2=4��
��3����Q���˶�ʱ����OMN�Ƕ�ֵ��
���ɣ���ͼ��ʾ��
��NE��MC��E����NF��OM��F����CG��x����G��
���ı���CGON�������Σ���CMF=��MFN=��NEM=90�㣬
���ı���EMFN�Ǿ��Σ�CG=OG=ON=CN=4����OCN=��CON=45�㣬
��CM��OQ��CN��y�ᣬ
���CMO=��CNO=90�㣬
��C��M��O��N�ĵ㹲Բ��
���OMN=��OCN=45�㣮
��Q���˶�ʱ����OMN�Ƕ�ֵ����ֵΪ45�㣮
���� �����Ƿ����������ۺ��⣬��Ҫ������ͼ����������������������������ʽ���������ε��ж������ʡ��ĵ㹲Բ�������ѶȽϴ��ۺ���ǿ���ر��ǣ�2���У���Ҫͨ����������֤�������Σ�


 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ʡ֦���о�У���꼶3��������ѧ�Ծ��������棩 ���ͣ��ж���
�� +��3x+y��1��2=0����
+��3x+y��1��2=0���� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABCO��ƽ���ı��Σ���OΪ����ԭ�㣬��A������Ϊ��-2��0������B��y����������ϣ���C��˫����y=-$\frac{8}{x}$�ϣ�ֱ��y=-x+m������C����x���ڵ�D��
��ͼ����ƽ��ֱ������ϵ�У��ı���ABCO��ƽ���ı��Σ���OΪ����ԭ�㣬��A������Ϊ��-2��0������B��y����������ϣ���C��˫����y=-$\frac{8}{x}$�ϣ�ֱ��y=-x+m������C����x���ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{7}$ | B�� | $\sqrt{9}$ | C�� | $\root{3}{27}$ | D�� | $\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ʡ֦���о�У���꼶3��������ѧ�Ծ��������棩 ���ͣ���ѡ��
��ͼ����ֱ֪��AB//CD��BEƽ�֡�ABC����CD��D����CDE=150�㣬���C�Ķ���Ϊ( ).

A. 120�� B. 130�� C. 150�� D. 100��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com