
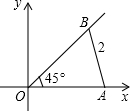
 在平面直角坐标系xOy中,点A是x轴正半轴上任意一点,点B是第一象限角平分线上一点(不含原点),AB=2,∠AOB=45°,以AB为一边作正△ABC,则
在平面直角坐标系xOy中,点A是x轴正半轴上任意一点,点B是第一象限角平分线上一点(不含原点),AB=2,∠AOB=45°,以AB为一边作正△ABC,则分析 (1)设△AOB的外接圆为⊙M,连接BM并延长交⊙M于点D,连接AD,然后只需证明△ABD为等腰直角三角形即可求得△AOB外接圆的半径.
(2)利用(1)的结论,设法证明△AOB外接圆的圆心到点O与点C的距离为定值,进而分析点C到原点O的距离的取值范围.
解答 解:(1)如下图所示:设△AOB的外接圆为⊙M,连接BM并延长交⊙M于点D,连接AD 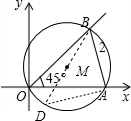
∵BD为⊙M的直径,
∴∠BAD=90°,
又∵∠BOA=∠BDA=45°(同弧所对的圆周角相等),
∴△ABD为等腰直角三角形.
∴AB=AD=2
∴BD=2$\sqrt{2}$
即:△AOB外接圆的半径是$\sqrt{2}$
故答案为:$\sqrt{2}$
(2)由(1)可知:△OAB的外接圆的半径为$\sqrt{2}$
设△OAB的外接圆的圆心为点M,则OM=$\sqrt{2}$,过点M做AB的垂直平分线,垂足为点N,连接AN,
∵△ABC是等边三角形,
∴AB的垂直平分线必经过点C
由垂径定理得:AN=$\frac{1}{2}$AB=1,MN=$\sqrt{2}$
∴由勾股定理得:MN=1,CN=$\sqrt{3}$,
∴CM=1+$\sqrt{3}$,
即:OM与CM的长度是定值,故只有点O、M、C三点共线时OC的长有最大值与最小值.
∴OC 的最小值为1+$\sqrt{2}$-$\sqrt{3}$,OC的最大值为1+$\sqrt{2}+\sqrt{3}$,
即:1+$\sqrt{2}$-$\sqrt{3}$≤OC≤1+$\sqrt{2}+\sqrt{3}$,
故答案为:1+$\sqrt{2}$-$\sqrt{3}$≤OC≤1+$\sqrt{2}+\sqrt{3}$,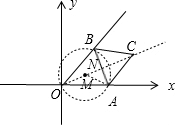
点评 本题考查了三角形的外接圆与外心、等边三角形的性质等问题,解(1)题的关键是将已知数据45°、2与△AOB的外接圆的半径或直径组合在同一个特殊三角形之中.解(2)的关键是证明OM与CM的长为定值.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
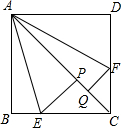 如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.
如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
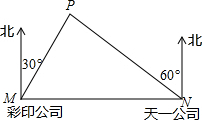 如图,我市计划在某工业园区内,为相距4千米的彩印公司、天一公司修一条笔直的公路,在彩印公司北偏东30°方向与天一公司北偏西60°方向的交点处,有一个以P为圆心,0.8千米为半径区域的住宅小区,问这条公路是否会穿越这个住宅小区?(参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}≈1.732$)
如图,我市计划在某工业园区内,为相距4千米的彩印公司、天一公司修一条笔直的公路,在彩印公司北偏东30°方向与天一公司北偏西60°方向的交点处,有一个以P为圆心,0.8千米为半径区域的住宅小区,问这条公路是否会穿越这个住宅小区?(参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}≈1.732$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
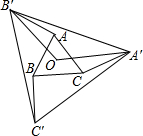 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com